STATISTIQUES
Ce document est un aide |
|
STATISTIQUES
Ce document est un aide |
|
Un test est un mécanisme qui permet de trancher entre deux
hypothèses au vu des résultats d'un échantillon.
Soient H0 et H1, ces deux hypothèses
(H0 est appelée hypothèse nulle, H1
hypothèse alternative), dont une et une seule est vraie. La décision
aboutira à choisir H0 ou H1. Il y a donc 4 cas
possibles schématisés dans le tableau suivant avec les
probabilités correspondantes :
Décision \ Vérité
|
H0
|
H1
|
H0
|
1 - a
|
b
|
H1
|
a
|
1 - b
|
a et b sont les probabilités d'erreur de première et deuxième espèce :
Il faut savoir que pour un échantillon d'effectif donné, la
valeur de a est inversement reliée avec
la valeur de b . Plus petites seront les
probabilités de commettre une erreur de type I, plus grandes seront
les probabilités de commettre une erreur de type II. La seule
manière de réduire simultanément les deux types d'erreur
est d'augmenter les effectifs des échantillons. Ainsi, de grands
échantillons résulteront des tests statistiques avec une puissance
(1 - b ) élevée.
On remarque que dans la plupart des articles de revues biologiques ou
médicales rapportant l'utilisation d'un test statistique la valeur
b n'est pas mentionnée.
Une des raisons souvent invoquée est la complexité du calcul
de la puissance (parfois le calcul est tout simplement impossible et beaucoup
de logiciels de statistiques n'en parlent même pas). Ainsi, même
s'il faisait preuve de la meilleure volonté, l'utilisateur du test
statistique se trouverait fréquemment dans l'impossibilité
de calculer la puissance (1 - b ) d'un test.
Ce point n'est pas sans conséquences. La disparition du risque
b interdit toute conclusion ferme quand, au bout
du compte, on ne peut rejeter l'hypothèse nulle. Dans ce cas, ne pas
rejeter l'hypothèse nulle signifie seulement qu'elle est acceptée
provisoirement parce que l'on ne peut pas faire autrement. Cela ne prouve
en aucune manière qu'elle est vraie. Par contre si l'on a calculé
le risque de seconde espèce b ,
a représente la force de la preuve requise
pour accepter l'hypothèse alternative, alors que
b permet de connaître la puissance de la
procédure et donc d'avoir une idée de la plausibilité
de l'hypothèse nulle quand celle-ci a été acceptée.
Test unilatéral ou bilatéral ?
Si l'hypothèse nulle correspond le plus souvent à une
égalité, il est des circonstances où l'hypothèse
alternative ne correspond pas à une inégalité du type
pA ¹ pB.
Pour un test bilatéral, nous pouvons émettre les hypothèses
suivantes :
Dans les tests unilatéraux, les hypothèses deviennent :
Hypothèse alternative, H1 : pA > pB.
1.1 Les tests paramétriques :
Un test est dit paramétrique si son objet est de tester certaine hypothèse relative à un ou plusieurs paramètres d'une variable aléatoire de loi spécifiée ou non. Dans la plupart des cas, ces tests sont basés sur la considération de la loi normale et supposent donc explicitement l'existence d'une variable aléatoire de référence X suivant une loi de Laplace-Gauss ou un effectif important (>30, >40, >50 ?...) (En effet, dès qu'une variable aléatoire est la somme d'un nombre "important" de variables aléatoires indépendantes, elle suit approximativement une loi normale (et ce, indépendamment de la loi des variables qui la génèrent). C'est pour cette raison que l'on peut souvent s'affranchir des hypothèses de normalité quand les effectifs étudiés sont importants.). La question se pose alors de savoir si les résultats restent encore valables lorsque X n'est pas normale : si les résultats sont valables, on dit que le test est robuste. La robustesse d'un test par rapport à un certain modèle est donc la qualité de rester relativement insensible à certaines modifications du modèle : on constatera que les tests sur les moyennes sont robustes.
1.1.1 Le test de Student :
Ce test permet de comparer une moyenne d'un échantillon à une
valeur donnée, de comparer les moyennes de deux échantillons
indépendants ou de deux échantillons appariés.
L'emploi de ce test reste subordonné en général à
deux conditions d'application importantes : la normalité et le
caractère aléatoire et simple des échantillons. La
première condition n'est toutefois pas essentielle lorsque les
échantillons ont des effectifs suffisants (en pratique, la valeur
de 30 est souvent retenue) pour assurer la quasi-normalité des
distributions d'échantillonnage des moyennes. En plus, de ces deux
conditions, nous devrons supposer, dans certains tests relatifs aux moyennes,
l'égalité des variances des échantillons
considérées.
1.1.1.1 Cas d'un seul échantillon :
Egalement appelé par certains auteurs test de conformité, ce
test a pour but de vérifier si l'échantillon à notre
disposition provient bien d'une population avec la moyenne spécifiée,
µ0, ou s'il y a une différence significative
entre la moyenne de l'échantillon et la moyenne présumée
de la population.
Exemple d'application :
Une usine veut vérifier le bon fonctionnement de ces machines. En
effet, l'usure des machines peut impliquer que l'usine ne suit plus les normes
imposées par tel ou tel organisme (l'Europe par exemple). Elle peut
utiliser ce test : elle va donc tirer aléatoirement un certain nombre
d'éléments de sa production, calculer sa moyenne et comparer
celle-ci avec la norme imposée.
Les hypothèses que l'on souhaite tester sont :
hypothèse nulle : H0 : µ = µ0
hypothèse alternative : Elle prend trois formes :
H1 : µ > µ0 (test unilatéral à droite)
H1 : µ < µ0 (test unilatéral à gauche)
H1 : µ ¹ µ0 (test bilatéral symétrique)
Conditions d'application du test de Student :
Le caractère de l'échantillon étant supposé
aléatoire, seule l'hypothèse de normalité de la variable
X doit être vérifiée par exemple avec le test de
Kolmogorov-Smirnov ou plus simplement graphiquement avec un histogramme ou
un diagramme de normalité tel la droite de Henry (que nous verrons
ultérieurement). Cependant, on admet que ceci est vrai pour un effectif
suffisamment important (n > 30).
Calcul :
Soit X une variable aléatoire distribuée selon un loi normale,
la variable aléatoire définie ci-dessus suit une loi de Student
avec n - 1 degrés de liberté.
tobs =
![]()
où µ0 est la moyenne de la population
spécifiée par H0,
![]() est la moyenne de
l'échantillon, S² est la variance de l'échantillon et
n la taille de l'échantillon
est la moyenne de
l'échantillon, S² est la variance de l'échantillon et
n la taille de l'échantillon
On compare la valeur calculée de t (tobs) avec la valeur
critique appropriée de t avec n - 1 degrés de
liberté. On rejette H0 si la valeur absolue de
tobs est supérieure à cette valeur critique.
Les valeurs critiques pour différents degrés de liberté
et différents seuils de signification sont donnés par la
table de Student. Pour un test unilatéral,
nous prendrons la valeur tn-1,1-a
de la table et pour un test bilatéral, nous prendrons
tn-1,1-a /2 . (La notation de
t varie selon les auteurs. Nous pouvons, par exemple, la trouver sous la
forme ta (2), n et
ta (1), n avec (2) et (1) correspondant
respectivement à un test bilatéral et à un test
unilatéral, et n étant le degré de
liberté)
Exemple :
On prélève entre deux marées 25 crabes sachant que la
température de l'air est de 24,3°C. On mesure la température
du corps. La question est de savoir si la température du corps est
identique à celle de l'air. Les données observées sont
les suivantes :
| 25,8 | 24,6 | 26,1 | 22,9 | 25,1 | 27,3 | 24,0 | 24,5 | |
| 23,9 | 26,2 | 24,3 | 24,6 | 23,3 | 25,5 | 28,1 | 24,8 | 23,5 |
| 26,3 | 25,4 | 25,5 | 23,9 | 27,0 | 24,8 | 22,9 | 25,4 |
Nous voulons tester les hypothèses :
La moyenne arithmétique des observations est égale à
: ![]() = 25,03 °C
= 25,03 °C
La variance est égale à : S² = 1,80 (°C)² (S²
= SCE / (n-1) avec SCE : Somme des Carrés des Ecarts).
Ces deux statistiques sont des estimations de la moyenne et de la variance
de la population à partir de laquelle a été tiré
cet échantillon. De plus, pour respecter les conditions d'application
du test de Student, cet échantillon a été
prélevé parmi beaucoup d'autres et au hasard dans la
population.
Nous supposons ici que les observations suivent une distribution normale
et calculons la valeur :
tobs =
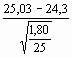 =
2.704
=
2.704
Le nombre de degrés de liberté associé au test est
égal à n - 1 = 24.
Si nous choisissons un seuil de signification a
de 5%, la valeur tn-1,1-a /2 de la
table de Student est égale à :
t9;0.975 = 2.064.
Comme |tobs| = 2.704 > 2.064, nous rejetons l'hypothèse
nulle et concluons qu'à un seuil de signification de 5%,
l'échantillon ne provient pas d'une population de moyenne µ =
24,3 °C.
Le problème peut être vu sous un autre angle. Avec les
paramètres en notre possession, nous pouvons définir un intervalle
de confiance de la moyenne µ de la population totale.
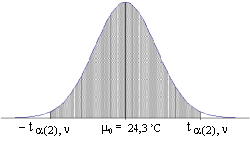
95% de la population se trouve dans la zone hachurée, soit :
µ0 - tn-1,1-a /2
![]() <
µ < µ0 + tn-1,1-a
/2
<
µ < µ0 + tn-1,1-a
/2 ![]()
Dans l'exemple, ci-dessus et en gardant a = 0.05, on a l'intervalle de confiance :
24.3 - 2.064 *
![]() <
µ < 24.3 + 2.064 *
<
µ < 24.3 + 2.064 *
![]()
23.75 < µ < 24.85
or ![]() qui est égal
à 25.03 °C est exclu de cet intervalle, donc l'échantillon
ne provient pas de cette population de moyenne 24.3 °C et de variance
(estimée) 1.80 (°C)².
qui est égal
à 25.03 °C est exclu de cet intervalle, donc l'échantillon
ne provient pas de cette population de moyenne 24.3 °C et de variance
(estimée) 1.80 (°C)².
Puissance du test :
Parfois, il est utile de connaître la puissance du test utilisé.
C'est notamment le cas, par exemple si l'hypothèse nulle n'a pas
été rejetée; rappelons que dans ce cas nous ne prouvons
en aucune manière que cette hypothèse est vraie. La puissance
d'un test correspond à la probabilité de mettre en évidence
une différence significative alors que celle-ci existe. Elle se calcule
en deux temps : d'abord la recherche de la valeur
tb (1), n
:
tb (1), n
= ![]() -
ta , n
= tobs - ta ,
n
-
ta , n
= tobs - ta ,
n
ta , n
est la valeur lue dans la table de Student
(ta (1), n
pour un test unilatéral et ta (2),
n pour un test bilatéral). Dans
un second temps, cette même table permet de convertir
tb (1), n
en b (risque de type II).
Néanmoins, pour une approche plus fine, il est préférable
d'utiliser la table de la distribution normale réduite fournissant
la fonction de répartition (Annexe 2). tb
(1), n est alors considérée
comme une approximation de Zb (1) qui,
grâce à la table, permet de déterminer
b et donc la puissance du test 1 -
b .
Dans notre exemple sur les crabes :
tb (1), n
= 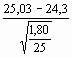 - 2.064 = 2.704 - 2.064 = 0.640
- 2.064 = 2.704 - 2.064 = 0.640
La table de Student fournit la valeur de
b : b > 0.25 donc
1 - b < 0.75.
Par celle de la loi normale, b = 0.2611 et la
puissance du test 1 - b est égale à
0.7389.
Ce qui veut dire qu'on a 26.1% de chances de faire une erreur de type II,
c'est-à-dire 73.9 % de chances de mettre en évidence une
différence significative (d'obtenir le résultat que l'on souhaite
démontrer). Pour améliorer la puissance d'un test,
l'expérimentateur peut, par exemple, augmenter l'effectif de son
échantillon.
1.1.1.2 Cas de deux échantillons indépendants :
Etant donné deux échantillons de taille n1 et
n2, peut-on admettre qu'ils ont été prélevés
dans une même population relativement à la variable
étudiée, ces deux échantillons ayant été
prélevés indépendamment l'un de l'autre ?
Les hypothèses à tester sont :
hypothèse nulle : H0 : µ1 = µ2
hypothèse alternative qui prend trois formes :
Conditions d'application :
Remarques :
Plusieurs auteurs ont montré que l'hypothèse de normalité
est d'importance relativement secondaire dans le test d'égalité
de deux moyennes. En effet, dans certaines limites, la non-normalité
des populations ne modifie pas sensiblement les risques d'erreur de
première et deuxième espèce. Ceci est vrai surtout pour
les distributions symétriques, même très différentes
des distributions normales.
De même, l'hypothèse d'égalité des variances n'est
pas fondamentale au point de vue pratique lorsque les effectifs des
échantillons sont égaux. En raison de cette faible
sensibilité du test à la non-normalité et à
l'inégalité des variances, on dira qu'il s'agit, pour des effectifs
égaux, d'un test robuste.
Par contre, lorsque les effectifs des échantillons sont inégaux,
il est absolument indispensable de s'assurer de l'égalité des
variances et, si cette hypothèse n'est pas vérifiée,
il est indispensable d'utiliser une méthode adaptée à
ces circonstances. On peut notamment procéder à une transformation
de variable, destinée à stabiliser les variances, et utiliser
ensuite le test de Student. Cependant, ce cas d'inégalité des
variances est assez rare (voir 2° remarques du chapitre 1.1.2 test de
Fisher).
Mode de calcul :
On calcule la valeur t observé (tobs) qui suit une variable
aléatoire de Student à (n =
n1 + n2 - 2) degrés de
liberté.
tobs =
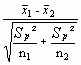
où ![]() et
et
![]() sont les moyennes des
deux échantillons, Sp² la variance commune.
sont les moyennes des
deux échantillons, Sp² la variance commune.
Cette dernière statistique correspond à la variance
s ² de la population parentale. Elle est
égale à :
Sp² =
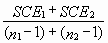 =
= ![]()
Si les effectifs des échantillons sont égaux, la valeur de t devient :
tobs =
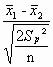
La valeur de t est comparée à la valeur critique
appropriée de t (dans la table de Student)
avec (n1 + n2 - 2) degrés
de liberté. On rejette H0 si la valeur absolue de
tobs est supérieure à cette valeur critique. Si
le test est unilatéral, nous prendrons la valeur
tn1 + n2 - 2,1-a
(ou ta (2), n
) de la table de Student. S'il est bilatéral, nous prendrons
la valeur tn1+n2-2,1-a /2 (ou
ta (1), n
).
Exemple :
Une étude est réalisée en vue de comparer l'efficacité
de deux fertilisants sur la croissance des plantes. On mesure la hauteur
de deux lots de plantes, chacun avec un fertilisant différent. Bien
sûr, nous avons cultivé la même espèce dans des
conditions environnementales identiques (ensoleillement, apports d'eau,
température …). Les données relevées sont les suivantes
:
Fertilisant 1 |
Fertilisant 2 |
||
| 48.2 cm 54.6 58.3 47.8 51.4 |
52.0 55.2 49.1 49.9 52.6 |
52.3 cm 57.4 55.6 53.2 51.3 |
58.0 59.8 54.8 |
Nous désirons savoir s'il existe une différence significative
entre les deux types de fertilisants, à un seuil de signification
de 1%.
Ceci implique les hypothèses suivantes :
hypothèse nulle H0 : µ1 ³ µ2 ou µ1 - µ2 ³ 0
Nous supposons à cet instant que les échantillons suivent une distribution normale et que l'égalité des variances a été vérifiée par un test de Fisher.
n1 = 10 |
n2 = 8 |
Sp² =
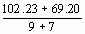 = 10.71 cm²
= 10.71 cm²
tobs =
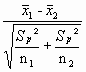 =
= 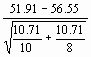 = -2.99
= -2.99
Le nombre de degrés de liberté associé au test est
égal à : ![]() = n1 + n2 - 2 = 16
= n1 + n2 - 2 = 16
La valeur de t théorique trouvée dans la table
de Student, pour a = 1% est :
ta (1),16 = 1.746
Comme la valeur absolue de t calculée est supérieure à cette valeur, tobs = |-2.99| > 1.746, nous rejetons l'hypothèse nulle au profil de l'hypothèse alternative, et concluons qu'à un seuil de signification de 1%, le deuxième fertilisant est plus efficace.
Puissance du test :
Pour mesurer la puissance d'un test, il faut dans un premier temps calculer
le paramètre suivant :
f =
![]()
avec n effectif "commun" des échantillons. Si les effectifs sont
inégaux n prend la valeur : n =
![]()
Les graphes de Pearson et Hartley fournissent à partir de
f la puissance du test recherchée.
Dans notre exemple précédent, les échantillons sont
d'effectifs inégaux, il faut donc calculer la valeur de n :
n = 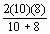 = 8.89
= 8.89
f =
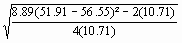 = 1.99
= 1.99
Consultons la table de Pearson et Hartley : pour un degré de liberté de 16, la puissance du test 1 - b = 0.48. Les chances de commettre une erreur de type II sont donc de 52 %.
1.1.1.3 Cas de deux échantillons appariés :
Le test de Student pour observations pairées sert à comparer
les moyennes de deux populations, dont chaque élément de l'une
des populations est mis en relation avec un élément de
l'autre.
Par exemple, il peut s'agir de comparer deux traitements, les données
étant considérées comme des paires d'observations
(première observation de la paire recevant le traitement 1 et
deuxième observation recevant le traitement 2).
Aspects mathématiques :
Soit xij l'observation j pour la paire i
(j = 1,2 et i = 1,2,...,n). Pour chaque paire d'observations on calcule la
différence di = xi2 - xi1.
Le test statistique est défini par :
tobs =
![]()
où n est le nombre de paires d'observations,
![]() est
la moyenne des différences entre les observations et
Sd² la variance.
est
la moyenne des différences entre les observations et
Sd² la variance.
Le test de Student pour observations pairées est un test bilatéral. Les hypothèses sont :
On rejette l'hypothèse nulle au seuil de signification
a si : |tobs| >
tn-1,1-a /2 où
tn-1,1-a /2 est la valeur de la
table de Student avec n - 1 degrés de
liberté.
Conditions d'application :
Exemple :
Supposons que deux traitements soient appliqués sur 10 paires
d'observations. Les données obtenues et les différences
correspondantes notées di se trouvent dans le tableau suivant
:
Paire |
Traitement |
||
I |
1 |
2 |
di = xi2 - xi1 |
1 |
110 |
118 |
8 |
La moyenne est égale à
![]() = 3.2
= 3.2
La variance est égale à Sd² = 36
Le test statistique est égal à : tobs =
![]() = 1.687
= 1.687
Si l'on choisit un seuil de signification a =
0.05, la valeur de t9;0.975 est 2.262. Par conséquent,
l'hypothèse nulle H0 : µ1 -
µ2 = 0 ne doit pas être rejetée puisque
|tobs| < t9;0.975 .
Puissance du test :
Pour calculer la puissance du test, on utilise la même procédure
que pour le cas d'un seul échantillon en remplaçant
![]() par
par
![]() et S² par
Sd². ce qui donne l'équation :
et S² par
Sd². ce qui donne l'équation :
tb (1), n
= ![]() - ta (2), n
- ta (2), n
Dans notre exemple : tb (1),
n = 1.687 - 2.262 = -0.575
Avec la table de Student, le risque
b de commettre une erreur de type II est
inférieur à 25%. Donc la puissance du test est supérieur
à 75%. Pour obtenir un résultat plus précis, la loi
normale nous donne la valeur b = 0.28 (la puissance
est donc égale à 0.72).
1.1.2 Le test de Fisher :
Utilisé pour tester l'égalité de deux variances, il
est très sensible à la non-normalité des échantillons
(on suppose aussi que les échantillons sont aléatoires et ont
été prélevés indépendamment les uns des
autres dans deux populations). Le principe de ce test est de calculer le
rapport des variances ci-dessous (avec la variance la plus grande au
dénominateur) et de la comparer à la variable donnée
par la table de Fisher-Snedecor avec n1 - 1 et n2 -
1 pour paramètres, correspondant aux degrés de liberté.
Fobs =
![]()
où n1 et n2 sont les effectifs des deux échantillons et S1² et S2² les variances.
Avec Fobs > 1
si Fobs £
F(n1-1,n2-1;1-a ) on accepte
l'hypothèse nulle H0 : s
1² = s 2²
(s 1² et
s 2² sont les variances des
populations "parentales") sinon on rejette H0.
Remarques :
Pour des effectifs égaux la valeur de F calculée se simplifie
:
Fobs =
![]()
Exemple :
avec n1 = 25, n2 = 13,
S1² = 0.05, S2² = 0.07 et
un seuil de signification a = 0.05,
peut-on accepter l'hypothèse nulle H0 :
s 1² =
s 2² ?
On suppose les conditions d'application valables.
Il faut d'abord permuter les indices 1 et 2 car
![]() >
>
![]()
Fobs =
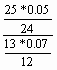 = 1.346 et F12;24 = 2.18 (lu dans la table de Fisher-Snedecor)
= 1.346 et F12;24 = 2.18 (lu dans la table de Fisher-Snedecor)
Fobs < Fthéor donc on accepte H0 : s 1² = s 2², on peut ensuite tester H0 : m 1 = m 2
1.1.3 Les coefficients de corrélation :
1) Le coefficient de corrélation de Bravais - Pearson :
Il permet de mesurer l'intensité de la liaison entre deux caractères
quantitatifs. C'est donc un paramètre important dans l'analyse des
régressions linéaires (simples ou multiples).
Il se calcule à partir de la covariance et des écart-types
: r = ![]()
Ce coefficient varie entre -1 et +1 :
Lorsque r est calculé sur un échantillon, on est amené
à tester sa significativité. Pour un risque d'erreur
a fixé, celle-ci varie en fonction du nombre
d'individus de la distribution. Quand ce nombre d'individus augmente, le
seuil inférieur de significativité s'abaisse.
La table fournit les valeurs r critiques au-delà
desquelles les coefficients de corrélation de Pearson obtenus sont
significatifs. Pour des échantillons de taille n, on prendra (n-2)
comme degré de liberté.
Remarques :
Il est fondamental de noter qu'une corrélation significative ne signifie
aucunement qu'il existe une relation de cause à effet entre les deux
variables. La corrélation peut en effet être liée à
une troisième variable, qui agit de manière indépendante
sur les deux premières. Pour contrôler l'influence d'autres
variables, il est nécessaire de procéder à des
corrélations partielles (voir ci-après).
De même, un faible coefficient de corrélation ne signifie pas
forcément l'indépendance des deux caractères. Il se
peut que la relation entre ces deux caractères soit non linéaire
(elle peut être parabolique, logarithmique ou exponentiel …).
La corrélation est à ce niveau essentiellement descriptive
(et non explicative).
2) Le coefficient de détermination r² :
Ce coefficient est le carré du coefficient de corrélation.
Il traduit la qualité d'une régression en résumant la
part de l'information totale prise en compte par le modèle de
régression.
r² =
![]()
Par exemple, r² = 0.87 : le modèle de régression prend en compte 87% de l'information contenue dans la distribution.
100%
|
=
|
87%
|
+
|
13%
|
Information totale
de la distribution Y |
Information prise en
compte par la régression |
Information résiduelle
|
3) Le corrélation multiple :
Le coefficient de corrélation multiple R exprime l'intensité
de la liaison entre la variable à expliquer et l'ensemble des variables
explicatives (nommées encore régresseurs).
4) Les corrélations partielles :
Comme énoncé précédemment, cette corrélation
exprime la liaison entre deux paramètres, en contrôlant l'influence
d'une troisième paramètre.
Par exemple, on peut rechercher la corrélation entre la taille et
le poids pour des sujets d'âge donné.
Pour trois variables, le coefficient de corrélation partielle peut
être calculée à partir des coefficients de corrélation
simple :
r12-3 =
![]()
Bien sûr, il est possible de calculer les deux autres coefficients
de corrélation partielle r13-2 r23-1.
Les calculs pour un nombre supérieur à trois variables sont
très lourds : l'emploi des ordinateurs est ici la bienvenue.
Un coefficient de corrélation partielle se teste comme un coefficient
de corrélation simple avec n - p - 1 degrés de liberté.
Ce coefficient est très utile lors des analyses de régressions
multiples. Au coefficient de corrélation multiple, il convient de
lui associer les coefficients de corrélation partielle. En effet,
quand les variables explicatives sont corrélées entre elles,
il est indispensable de connaître les coefficients de corrélation
partielle entre la variable à expliquer (Y) et chacune des variables
explicatives (X1, X2,
X3…Xj). Un coefficient de corrélation partielle
entre Y et un des régresseurs indique l'intensité de la relation
spécifique, compte tenu des autres variables explicatives
présentes.
Par exemple, si l'on recherche pour un ensemble de stations (individus),
la liaison entre la production de la biomasse (Y), la pluviosité
(X1) et l'ensoleillement (X2), pluviométrie
et ensoleillement étant partiellement liée, il est difficile
de connaître le rôle de chacun des deux facteurs retenus. Le
coefficient de corrélation partielle entre Y et X1 indique
l'intensité de la relation entre biomasse et pluviosité, en
maintenant l'ensoleillement constant (la variable X2 est prise
en compte). Un coefficient de corrélation partielle est donc défini
en fonction des autres régresseurs.
5) Comparaison de coefficients de corrélation de Bravais - Pearson
:
La comparaison de coefficients de corrélation n'est possible que si
ces coefficients suivent une distribution normale. Il est donc nécessaire,
dans un premier temps, de normaliser les coefficients de corrélation
en utilisant la transformation de Fisher. On applique la formule :
z = ![]()
Alors que r varie de -1 à +1, z varie entre 0 et ¥ .
Cette transformation normalise les coefficients de corrélation mais
présente un autre avantage : elle permet de stabiliser la variance
de la distribution initiale.
Pour comparer deux coefficients de corrélation, on calcule : Z =
![]() où
où
![]() =
=
![]()
n1 et n2 étant les effectifs de chacun des échantillons impliqués dans le calcul des coefficients de corrélation.
Si n1 = n2 alors
![]() =
= ![]()
La valeur de Z suit une distribution de Student. Comme pour une comparaison de deux moyennes, si on choisit un test bilatéral, l'hypothèse nulle correspond à r1= r2 et l'hypothèse alternative à r1 ¹ r2 . On apprécie la signification de la valeur de Z avec celle lue dans la table de Student (Za (2) = ta (2), ¥ ). Ici, le degré de liberté est égal à l'infini.
Exemple :
Ho : r1 = r2 |
HA : r1 ¹
r2 |
Par la transformation de Fisher :
z1 = 1.0454 |
z2 = 1.2212 |
Z = 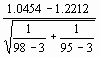 =
-1.202
=
-1.202
avec ![]() = 0.1463
= 0.1463
Dans la table de Student, on lit Z0.05(2) = t0.05(2),
¥ = 1.960
Donc nous ne rejetons pas l'hypothèse nulle.
Puissance du test :
Pour obtenir la puissance 1 - b du test, il faut
d'abord calculer : Zb (1) =
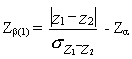 -
Za
-
Za
puis lire la valeur de b dans la table de la loi
normale réduite. En reprenant l'exemple ci-dessus,
Zb (1) =
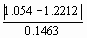 - 1.960 = -0.76
- 1.960 = -0.76
b = P (Z ³ -0.76)
= 1 - P (Z £ -0.76) = 1 - 0.2232 = 0.78 soit
78 % de chances de commettre une erreur de type II.
La puissance du test 1 - b est de 0.22.
6) Comparaison de plusieurs coefficients de corrélation de Bravais
- Pearson :
ZAR (p 384) : Méthode de Paul puis si nécessaire
méthode de Tukey
1.1.4 Le test d'indépendance du chi-carré :
Le test d'indépendance du chi-carré vise à déterminer
si deux variables observées sur un échantillon sont
indépendantes ou non. Les variables étudiées sont des
variables qualitatives catégorielles.
Le test d'indépendance s'effectue sur la base d'une table de
contingence.
Exemple :
On cherche à déterminer si le fait de fumer est indépendant
du sexe des individus.
Les deux variables à étudier sont des variables qualitatives
catégorielles qui compte deux catégories chacune :
La table de contingence obtenus à partir d'un échantillon de 100 individus (n = 100) est la suivante :
|
Fumer
|
|||
"fume"
|
"ne fume pas"
|
Total
|
||
Sexe
|
M
|
21
|
44
|
65
|
F
|
10
|
25
|
35
|
|
Total
|
31
|
69
|
100
|
|
Notons nij (i = 1, 2, j = 1, 2) les fréquences
observées.
Nous allons estimer les fréquences de chaque case du tableau sous
l'hypothèse de l'indépendance entre les deux variables. Notons
eij, ces fréquences estimées :
eij =
![]()
Nous obtenons : e11 =
![]() = 20.15 e12 =
= 20.15 e12 =
![]() = 44.85 et e21 =
= 44.85 et e21 =
![]() = 10.85 e22 =
= 10.85 e22 =
![]() = 24.15
= 24.15
En définitive, le tableau de fréquences estimées est le suivant :
|
Fumer
|
|||
"fume"
|
"ne fume pas"
|
Total
|
||
Sexe
|
M
|
20.15
|
44.85
|
65
|
F
|
10.85
|
24.15
|
35
|
|
Total
|
31
|
69
|
100
|
|
Si l'hypothèse nulle H0 est vraie, la statistique
c ² =
![]()
suit une loi du chi-carré avec (r-1)(c-1) degrés de liberté, où r est le nombre de lignes et c le nombre de colonnes du tableau. Dans notre exemple, nous avons donc (2-1)(2-1) = 1 degré de liberté et c ² = 0.036 + 0.016 + 0.066 + 0.030 = 0.148
En choisissant un seuil de signification de 5%, la valeur
![]() de
la table de chi-carré est égale à 3.84.
de
la table de chi-carré est égale à 3.84.
Comme la valeur de c ² calculée est
nettement inférieure à la valeur trouvée dans la table
du chi-carré, nous ne rejetons pas l'hypothèse nulle et concluons
que les deux variables étudiées sont indépendantes.
1.2 Les tests non paramétriques :
Un test non paramétrique est un test d'hypothèse pour lequel
il n'est pas nécessaire de spécifier la forme de la distribution
de la population étudiée. Il faut cependant en général
que les observations soient indépendantes, c'est-à-dire que
la sélection d'un quelconque individu dans la population en vue de
former l'échantillon ne doit pas influencer le choix des autres
individus.
Les méthodes non paramétriques requièrent peu
d'hypothèses concernant la population étudiée. Elles
ignorent notamment l'hypothèse classique de la normalité
de la population.
Ces tests peuvent être appliquer à de petits
échantillons.
Ils peuvent s'appliquer à des caractères qualitatifs, à
des grandeurs de mesure, à des rangs de classement ...
Ils peuvent s'appliquer à des données incomplètes ou
imprécises.
Des recherches théoriques ont montré que l'efficacité
des tests non paramétriques n'est que légèrement
inférieure à celle de leurs équivalents paramétriques
quand la distribution de la population étudiée est
spécifiée, par exemple la loi normale. Elle est en revanche
supérieure à celle des tests paramétriques quand la
distribution de la population dévie sensiblement de la distribution
spécifiée (normale).
1.2.1 Méthodes graphiques et tests statistiques permettant de
vérifier la normalité d'un échantillon
Rappels : La loi normale, ou Loi de Gauss ou encore de Laplace-Gauss est
la loi d'une variable X continue, variant de -
¥ à +
¥ , dont la densité de probabilité
f(x) est :
f(x) = ![]()
La loi normale dépend de deux paramètres : la moyenne m et l'écart-type s .
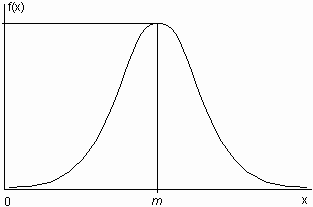
La courbe représentative de f(x) est "la courbe en cloche",
symétrique par rapport à x = m.
Cette loi normale est notée
N (m, s ). La fonction de répartition est
:
F(x) =
![]()
Toute loi normale
N (m,
s ) se ramène par le changement de
variable à une loi normale de moyenne nulle et
u =
![]()
d'écart-type unité, dite loi normale réduite N (0, 1) dont les fonctions de densité de probabilité f(u) et de répartition F(u) sont :
f(u) =
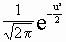 et F(u) =
et F(u) =
![]()
Grâce aux tables de la loi normale réduite, il est possible
de répondre à toutes les questions que l'on peut se poser à
propos d'une loi normale N
(m, s ) quelconque.
On peut ainsi déterminer la probabilité P pour que la variable
X soit comprise dans un certain intervalle, en tirant partie de la formule
résultant du changement de variable
u = ![]() avec u1 =
avec u1 =
![]() et
u2 =
et
u2 =
![]()
P(x1 < X £ x2) = F(x2) - F(x1) = F(u2) - F(u1)
La symétrie de la fonction f(x) permet de simplifier la table donnant les valeurs F(u) en retenant seulement les valeurs pour u ³ 0 de sorte que pour une valeur négative "-u1", on a :
F(-u1) = 1 - F(u1)
Exemple : dans la loi N (m = 12, s = 2), calculer P(8.5 < X £ 15)
P(8.5 < X £ 15) = P(u1 <
![]() £ u2) avec : u1 =
£ u2) avec : u1 =
![]() = -1.75 et u2 =
= -1.75 et u2 =
![]() = 1.5
= 1.5
P(-1.75 <
![]() £ 1.5) = F(1.5) - F(-1.75).
£ 1.5) = F(1.5) - F(-1.75).
Or F(-1.75) = 1 - F(1.75), dans la table de la loi normale réduite, nous lisons la valeur F(1.75) = 0.9599.
F(-1.75) = 1 - 0.9599 = 0.041 et F(u2 = 1.5) = 0.9332
P(8.5 < X £ 15) = F(u2) - F(u1) = 0.9332 - 0.041 = 0.8922 = 89.22 %
Ce qui veut dire qu'il y a 89.22 % de chances d'avoir 8.5 < X £ 15.
Exemple 2 : si X suit la loi
N (3.5;2),
on a :
P(X £ 4) =
P(![]() £
£
![]() )
= P(
)
= P(![]() £ 0.25) = F(0.25) = 0.5987
£ 0.25) = F(0.25) = 0.5987
F(0.25) a été lue dans la table et cela signifie qu'il y a
59.87 % de chances d'avoir X £ 4.
Exemple 3 : si X suit la loi
N (50,4),
on a :
P(40 £ X £
60) = P(-2.5 £
![]() £ 2.5) = F(2.5) - F(-2.5) = 2 F(2.5) - 1
= 0.988.
£ 2.5) = F(2.5) - F(-2.5) = 2 F(2.5) - 1
= 0.988.
Exemple 4 : si X suit la loi
N (0,1),
on a :
P(-3 £ X £
3) = F(3) - F(-3) = 2 F(3) - 1 = 0.997 = 99.7 %
Le fait que P(-3 £ X
£ 3) = 99.7 % montre que pratiquement toute
la probabilité est concentrée dans l'intervalle [-3,3]. Ceci
est lié à la décroissance rapide de la densité
f(x) lorsque x à ±
¥ .
Les paragraphes suivants montrent des méthodes permettant de vérifier la normalité d'un échantillon.
1.2.1.1 La droite de Henry :
C'est une procédure pratique et rapide, permettant de vérifier
la présomption de normalité pour une population dont on observe
un échantillon.
Cette procédure graphique ne constitue pas, à proprement parler,
un test statistique. Néanmoins, le tracé d'un graphique de
Henry peut suffire dans de nombreux cas où l'on doit s'assurer de
la normalité d'une distribution d'échantillonnage.
Le principe de la méthode repose sur la liaison linéaire
entre une variable normale x (moyenne m, écart-type
s ) et la variable réduite u (on rappelle
que u =
![]() ).
).
1.2.1.2 Les tests de normalité :
a) Le test de Kolmogorov-Smirnov
Dans le cas général, le test de Kolmogorov-Smirnov vise à
déterminer si les fonctions de répartition de deux populations
sont identiques. Il est utilisé lorsqu'on est en présence de
deux échantillons provenant de deux populations pouvant être
différentes. Contrairement au test de Mann-Whitney ou au test de Wilcoxon
(cf paragraphes 1.2.2 et 1.2.3) dont l'objet est de détecter des
différences entre deux moyennes ou médianes, le test de
Kolmogorov-Smirnov a l'avantage de prendre en considération les fonctions
de répartitions dans leur ensemble.
Mais le test de Kolmogorov-Smirnov peut aussi être utilisé comme
test d'adéquation. Dans ce cas, on est en présence d'un
seul échantillon aléatoire tiré d'une population; sa
fonction de répartition sera comparée à une fonction
de répartition spécifique et connue (par exemple celle de
la loi normale, celle de la loi uniforme ou encore celle de la loi de
chi-carré).
Exigences :
les deux échantillons sont des échantillons aléatoires tirés de leur population respective.
il y a indépendance mutuelle entre les deux échantillons.
les variables aléatoires doivent être continues, sinon le test est moins précis. Si ces variables sont qualitatives, il vaut mieux utiliser le test de chi-carré.
b) Le test de Lilliefors
Alors que le test de Kolmogorov-Smirnov permet de comparer la fonction de
répartition d'une variable aléatoire centrée et
réduite à celle de la loi normale de moyenne nulle et
d'écart-type unité; celui de Lilliefors compare la fonction
de répartition d'une variable aléatoire quelconque à
celle d'une loi normale de moyenne et d'écart-type non
spécifiée (m et
s ).
Un des avantages des tests de Kolmogorov-Smirnov et Lilliefors est leur possible
utilisation quel que soit l'effectif de l'échantillon. Cependant ces
tests sont de plus en plus considérés comme des méthodes
pauvres et donc non recommandés.
Zar propose d'utiliser la méthode de Shapiro et Wilk ou encore celle
d'Agostino et Pearson. Pour chacune de ces deux méthodes, la puissance
est excellente. Cependant, bien que pouvant être employée pour
des petits échantillons, la méthode de Shapiro et Wilk voit
sa puissance altérée lorsque les données présentent
des doublons. Zar conseille plus particulièrement le test d'Agostino
et Pearson excellent pour des échantillons avec un effectif d'au moins
20 mesures.
c) Le test d'Agostino - Pearson :
Il s'appuie sur les coefficients d'asymétrie et d'aplatissement.
L'hypothèse nulle d'une population normale est testée en utilisant
la statistique : K² =
![]() +
+
![]()
![]() permet
de tester l'asymétrie,
permet
de tester l'asymétrie,
![]() l'aplatissement.
l'aplatissement.
On regarde si K² suit une distribution de c
² avec n = 2 comme degrés de liberté
et a = 0.05.
Si la valeur K² est supérieure à celle lue dans la table
: on rejette HO. Si elle est inférieure, on accepte
HO.
En annexe, je donne les calculs des valeurs de
![]() et
de
et
de ![]() .
.
d) Changements de variables :
Si un de ces tests aboutit à une distribution non normale de la variable
aléatoire ou si le graphique de Henry montre une relation non
linéaire, il peut être intéressant dans ces cas d'examiner,
par ces mêmes méthodes, si un changement de variable, par exemple
y = log10x ou y =
![]() ,
conduit à un distribution normale de la variable transformée
y.
,
conduit à un distribution normale de la variable transformée
y.
1.2.2 Le test de Mann-Whitney :
C'est un test non-paramétrique qui permet de tester les moyennes de
deux échantillons indépendants. La réalisation du test
est basée sur le classement dans un ordre croissant de l'ensemble
des observations. Ici, ce n'est donc pas indispensable que les échantillons
suivent une distribution normale : des distributions symétriques suffisent
à valider le test. Ce test est un cas particulier du test de
Kruskall-Wallis.
1.2.3 Le test de Wilcoxon :
C'est aussi un test sur les rangs mais il permet de tester les moyennes de
deux échantillons associés par paires. Là aussi, des
distributions symétriques suffisent. Ce test est un cas particulier
du test de Friedman.
1.2.4 Le test de Kruskall-Wallis :
Ce test est préféré à l'analyse de variance à
un facteur lorsque les hypothèses de normalité des différents
échantillons ne sont pas respectées. Il vise à tester
l'égalité de plusieurs populations mais indépendantes.
C'est toujours un test sur les rangs comme l'est aussi le test suivant.
1.2.5 Le test de Friedman :
Ce test est utilisé pour tester l'égalité de plusieurs
populations appariées lorsque l'analyse de variance ne peut être
utilisée toujours pour des raisons d'hypothèses de normalité
non respectées ou de faibles effectifs.
1.2.6 Le test du coefficient de corrélation de Spearman :
Il correspond à l'équivalent non-paramétrique du test
basé sur le coefficient de corrélation de Pearson et est
également un test sur les rangs.
Les coefficients de corrélation des rangs sont très utiles
pour tester l'indépendance de deux variables non normales ou lorsque
l'échantillon est petit : on sait en effet qu'on ne peut appliquer
le test du coefficient de corrélation linéaire de Pearson.
Les tests de corrélation sont alors les seuls applicables, car ils
ne dépendent pas de la distribution normale.
De plus ils sont robustes car insensibles à des valeurs aberrantes.
Bien sûr ces tests peuvent être appliquer dans le cas de variables
ordinales.
La table de Spearman fournit les valeurs critiques
au-delà desquelles les coefficients de corrélation de Spearman
obtenus sont significatifs. Pour des échantillons de taille n, on
prendra n comme degrés de liberté.
1.2.7 Le test de corrélation des rangs de Kendall :
C'est l'équivalent du test du coefficient de corrélation de
Spearman mais pour des observations appariées.
L'analyse de variance (ANOVA pour Analysis Of VAriance) regroupe un ensemble
de techniques de tests et d'estimation visant à optimiser des protocoles
expérimentaux pour individualiser l'influence de différents
facteurs sur un paramètre à mesurer et revient dans le
cas simple à comparer plusieurs moyennes d'échantillons
gaussiens.
Ces différentes techniques sont le reflet formel de plans
d'expérience conçus préalablement et pouvant être
diversifiés à l'infini au gré de l'astuce des
expérimentateurs. De ce fait, il existe différentes techniques
d'analyse de variance. Citons quelques exemples typiques :
Les variables qualitatives susceptibles d'influer sur la distribution de la variable numérique observée sont appelées "facteurs de variabilité" et leurs modalités "niveaux". Lorsqu'il y a plusieurs facteurs, une combinaison de niveaux est un "traitement".
2.1 L'analyse de variance à un facteur de variabilité
:
Il s'agit ici d'étudier l'influence d'un seul facteur de variabilité
sur un paramètre quantitatif, ce qui revient à comparer les
moyennes de plusieurs populations supposées normales et de même
variance à partir d'échantillons aléatoires simples
et indépendants les uns des autres. Cette analyse peut être
considérée comme une généralisation du test de
Student.
Pourquoi délaisser le test de Student : si l'on compare toutes les
moyennes entre elles, il est nécessaire de réaliser p(p-1)/2
tests. Chacun de ces tests étant susceptibles de conclure de façon
non appropriée à une différence significative, le risque
global de trouver une telle différence à tort devient bien
supérieur au 5% que l'on octroie habituellement. Démonstration
:
(1 - .05) = .95
.95 * .95 * .95 = .953 = 0.86
De manière plus générale pour k épreuves
indépendantes chacune évaluées avec un seuil
a , la probabilité de ne pas commettre
d'erreur de type I sur cette famille sera donnée par la formule :
(1 - a )k avec k, nombre de
comparaisons par paires.
Par conséquent, la probabilité de commettre au moins une erreur
de type I sur la famille de comparaisons (chacune évaluée au
seuil a ) s'obtient par : 1 - 0.86 = 0.14, plus
généralement par :
1 - (1 - a )k.
p moyennes |
k comparaisons |
.05 |
.01 |
2 |
1 |
.05 |
.01 |
Il est donc indispensable d'utiliser une analyse de variance qui permet de
réduire ce risque d'erreur.
Procédure d'une analyse de variance :
La comparaison des moyennes se fait en deux étapes :
Conditions nécessaires à la validité de l'analyse de variance :
Rappelons qu'un histogramme ou un diagramme de normalité tel la droite
de Henry peut suffire à vérifier le bien fondé des
conditions de normalité.
La dernière condition est d'ordinaire satisfaite en utilisant une
procédure "d'aléatorisation" (ou de randomisation). Procédure
pour laquelle on affecte au hasard chaque individu à un groupe
expérimental.
En ce qui concerne l'hypothèse de normalité, des études
ont permis de conclure que l'analyse de variance est peu sensible, dans
l'ensemble, à la non-normalité des populations
considérées. Il suffit en pratique d'éviter d'employer
l'analyse de variance lorsque les distributions des populations parents sont
très différentes des distributions normales (distributions
en i ou en j par exemple), et lorsque les distributions sont de formes fort
différentes d'une population à l'autre (distribution en cloche
à dissymétrie de sens opposés par exemple), surtout
pour de petits échantillons.
De même, l'hypothèse des variances ou hypothèse
d'homoscédasticité est d'importance relativement secondaire
lorsque les effectifs des échantillons sont tous égaux. Dans
ces conditions, l'analyse de variance est, comme pour le test de Student,
une méthode robuste, tant en ce qui concerne la normalité qu'au
point de vue de l'égalité des variances.
Il n'en est cependant pas ainsi quand les effectifs des échantillons
sont variables. Le risque de première espèce peut alors être
influencé considérablement par une inégalité
des variances, surtout lorsque les échantillons d'effectifs les plus
réduits correspondent aux populations de variances maximums.
Quand certaines des conditions d'application sont loin d'être satisfaites,
on peut tout d'abord essayer de s'en rapprocher en effectuant l'une ou l'autre
transformation des variables : certaines de ces transformations permettent
en effet de normaliser dans une certaine mesure les distributions et de
stabiliser leurs variances. Si cette façon ne donne pas satisfaction,
on peut aussi utiliser des tests non paramétriques, qui ne sont pas
soumis à de telles restrictions en ce qui concerne leurs conditions
d'utilisation.
Rappels : principes et réalisation d'une analyse de variance
Désignons par xik les différentes valeurs
observées, le symbole xik représentant d'une
manière générale la kème observation
(k = 1, ..., ni) de l'échantillon extrait de la
ième population (i = 1, ..., p). Et désignons
respectivement par
![]() i et
i et
![]() les moyennes des
différents échantillons et de la moyenne générale
:
les moyennes des
différents échantillons et de la moyenne générale
:
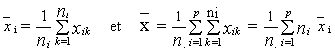
- Le modèle observé de l'analyse de variance à un facteur de classification s'écrit pour chaque valeur observée xik :
xik -
|
(1)
|
variation totale = variation factorielle + variation résiduelle
Cette relation signifie que les écarts par rapport à la moyenne générale (variation totale) se divisent en deux composantes : les écarts des moyennes des échantillons par rapport à la moyenne générale (variation factorielle) et les écarts existant à l'intérieur des échantillons (variation résiduelle).
Le modèle théorique de l'analyse de variance s'écrira
:
(Xik - m) = (mi - m) + (Xik -
mi)
ou Xik = m + ai + e
ik
avec Xik : représente la variable dépendante, m
: la moyenne générale de la population parentale, elle est
estimée par ![]() ,
la moyenne de l'ensemble des échantillons ; ai : les
écarts factoriels, ai = mi - m, existant entre
les moyennes théoriques mi des différentes populations
(ces moyennes mi sont estimées par les moyennes
,
la moyenne de l'ensemble des échantillons ; ai : les
écarts factoriels, ai = mi - m, existant entre
les moyennes théoriques mi des différentes populations
(ces moyennes mi sont estimées par les moyennes
![]() i des
échantillons) et la moyenne m de la population parentale. Les
quantités ai sont souvent appelées effets du facteur
contrôlé ou effets principaux ; e
ik : les écarts résiduels
(e ik = xik -
mi). e ik correspond à
l'erreur expérimentale de l'observation xik. Ils suivent
une distribution de Gauss
N (0, s )
i des
échantillons) et la moyenne m de la population parentale. Les
quantités ai sont souvent appelées effets du facteur
contrôlé ou effets principaux ; e
ik : les écarts résiduels
(e ik = xik -
mi). e ik correspond à
l'erreur expérimentale de l'observation xik. Ils suivent
une distribution de Gauss
N (0, s )
Et l'hypothèse nulle Ho à tester se présente sous la forme :
Si les écarts factoriels (= effets principaux) sont nuls alors il
n'existe pas d'effet groupe.
Cette hypothèse est testée après avoir calculée
la valeur F de Fisher-Snedecor et comparée à une valeur
théorique trouvée dans la table de Fisher-Snedecor. Cette valeur
F se calcule de la manière suivante :
- En élevant au carré les deux membres de l'identité
(1) et en les sommant pour toutes les valeurs observées, on obtient
l'équation d'analyse de variance :
![]() (xik
-
(xik
- ![]() )² =
)² =
![]() (
(![]() i -
i -
![]() )² +
)² +
![]() (xik
-
(xik
- ![]() i)²
i)²
SCEt = SCEa + SCEr
La somme des carrés des écarts totale est divisée en deux composantes additives : une somme des carrés des écarts factorielle ou entre échantillons et une somme des carrés des écarts résiduelle ou dans les échantillons.
Les carrés moyens concernant la variation factorielle sont égaux
à : CMa = SCEa / (p - 1)
Les carrés moyens concernant la variation résiduelle sont
égaux à : CMr = SCEr / (n - p). Nous
verrons ci-après que cette valeur intervient dans la méthode
de la plus petite différence significative.
Le rapport CMa / CMr correspond à la valeur
Fobservée. C'est aussi le rapport
![]()
C'est ce rapport qui est comparé à la valeur
Fthéorique lue dans la table de Fisher-Snedecor avec p
- 1 et n - p degrés de liberté.
Tableau récapitulatif :
| Variation Totale | Variation factorielle | Variation résiduelle | |||
| Modèle observé | xik -
|
= | + | Xik -
|
|
| Equation d'analyse de variance | (ou SCEt) |
= | (ou SCEa) |
+ | (ou SCEr) |
| Nombre de degrés de liberté | n – 1 | = | p – 1 | + | n – p |
| Carrés moyens | SCEt / (n - 1) (ou CMt) |
SCEa / (p - 1) (ou CMa) |
SCEr / (n - p) (ou CMr) |
||
| Modèle théorique | Xik - m | = | mi – m | + | Xik - mi |
| F observé | F = CMa / CMr |
Remarques :
Dans une analyse de variance, un facteur peut être à effet fixe
ou à effet aléatoire.
Un facteur à effet fixe est un facteur dont les modalités ne
changent pas quand l'expérience considérée est
réalisée à plusieurs reprises. Si, par exemple, on compare
quatre variétés de maïs cultivées chacune sur six
parcelles de terre; dans une telle situation, le facteur "variété"
est à effet fixe, car si l'on désire dupliquer l'expérience,
cela n'a pas de sens de modifier les variétés de maïs
à comparer. A l'opposé, les six parcelles de terre étant
tirées au sort parmi un vaste lot de terres, on peut imaginer qu'une
nouvelle expérience conduise à une nouveau tirage au sort,
les parcelles ne seraient nécessairement plus les identiques... Dans
un tel cas, le facteur "parcelle" est, par définition, aléatoire.
On pourrait néanmoins tout aussi bien décider de conserver
les six parcelles retenues pour la première expérience, le
facteur "parcelle" serait alors fixe, au même titre que le facteur
"variété".
De ce fait, il existe deux modèles :
Modèle I : ANOVA à un facteur fixe
Modèle II : ANOVA à un facteur aléatoire
Dans le cas de l'analyse de variance à un facteur, la distinction entre ces deux modèles n'est pas essentielle. Par contre, elle l'est lors des analyses de variance à deux facteurs.
Puissance de l'analyse de variance à un facteur :
Si l'ANOVA montre qu'il n'y a pas d'effet du facteur étudié,
il peut être utile de connaître la probabilité de commettre
une erreur de type II (b ).
Le calcul de la puissance se fait en deux temps : le calcul du paramètre
f , puis la consultation des graphes de Hartley
et Pearson.
f =
![]()
avec p : nombre de populations.
Exemple numérique :
p = 3 n1 = n2 = 4 n3 = 5
H0 : m 1 =
m 2 = m
3
Formes de variations
|
Somme des carrés
|
Degrés de liberté
|
Carrés moyens
|
Totale
|
26.9231
|
12
|
|
Factorielle
|
10.3721
|
2
|
5.1866
|
Résiduelle
|
16.5500
|
10
|
1.6550
|
F = 3.13 F0.05(1), 2, 10 = 4.10 H0 non rejetée, la puissance peut être calculée :
f =
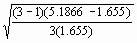 = 1.19
= 1.19
avec p = 3, n 1 = 2 et n 2 = 10, on lit dans les graphes de Hartley et Pearson pour f = 1.19 : 1 - b = 0.33. donc il y a 67 % de chances de commettre une erreur de type II (Rappelons que b est la probabilité d'accepter l'hypothèse nulle alors que c'est l'hypothèse alternative qui est vraie.).
Comparaisons de plusieurs moyennes :
Rappelons que les comparaisons de plusieurs moyennes (c'est-à-dire
les tests post hoc) ne peuvent être réalisées que si
l'analyse de variance montre un effet significatif du facteur étudié.
Comme précisé précédemment il n'existe pas de méthodes "idéales". Plusieurs permettent d'effectuer toutes les comparaisons de moyenne deux à deux, ce sont celles de :
Dans les suivantes, seules une partie de l'ensemble des comparaisons de moyenne deux à deux seront effectuées.
Dans l'exposé des différentes méthodes de comparaison, nous supposerons toujours que les conditions de base de l'analyse de variance sont satisfaites tant en ce qui concerne le caractère aléatoire et simple des échantillons que la normalité et l'égalité des variances des populations parents. Cette dernière condition s'avère particulièrement importante dans les problèmes de comparaisons multiples. Nous supposerons en outre, généralement, que les échantillons considérés sont tous de même effectif.
2.1.1 - le test Least Significative Difference (LSD)
Cette méthode permet de comparer toutes les moyennes deux à
deux grâce au test de Student.
On rappelle que tobs =
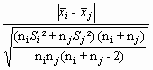 ou =
ou =
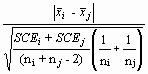
Toutefois, puisqu'en réalisant l'analyse de variance, on a supposé
que les variances de toutes les populations étaient égales,
il ne se justifie pas de rechercher pour chacune de ces comparaisons une
nouvelle estimation de la variance commune. Il est préférable
d'employer dans tous les cas l'estimation globale fournie par le carré
moyen résiduel (CMr).
D'autre part, lorsque les effectifs sont égaux, au lieu de calculer
les p(p - 1)/2 valeurs de tobs et de rejeter l'hypothèse
d'égalité des moyennes chaque fois que :
tobs =
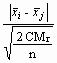 ³ t1 - a /2 ,
il est plus facile de calculer une fois pour toutes la quantité :
t1 - a /2
³ t1 - a /2 ,
il est plus facile de calculer une fois pour toutes la quantité :
t1 - a /2
![]() ,
,
et de rejeter l'hypothèse d'égalité des moyennes chaque
fois que la différence
|![]() i -
i -
![]() j | est
supérieure ou égale à cette quantité. Cette
expression est appelée la plus petite différence
significative.
j | est
supérieure ou égale à cette quantité. Cette
expression est appelée la plus petite différence
significative.
Inconvénient de la méthode : cette approche s'appuie sur le
test de Student. Or, comme nous l'avons dit dans l'introduction relative
à l'analyse de variance à un facteur, si l'on compare toutes
les moyennes entre elles, il est nécessaire de réaliser p(p-1)/2
tests. Et donc, chacun de ces tests étant susceptibles de conclure
de façon non appropriée à une différence
significative, le risque global de trouver une telle différence à
tort devient bien supérieur au 5% que l'on octroie habituellement.
Il est donc indispensable d'utiliser d'autres méthodes qui permettent
de réduire ce risque d'erreur. Plusieurs méthodes ont
été proposées par différents auteurs : Bonferonni,
Newman-Keuls, Tukey, Duncan pour palier cet inconvénient.
2.1.2 - le test de Bonferonni :
Appelé aussi "test du t-corrigé", le test de Bonferonni permet
de réaliser toutes les comparaisons deux à deux des moyennes
c'est-à-dire
![]() comparaisons avec p populations groupes (ou p niveaux) en
respectant globalement le risque a choisi : chacune
des comparaisons est effectuée au risque
comparaisons avec p populations groupes (ou p niveaux) en
respectant globalement le risque a choisi : chacune
des comparaisons est effectuée au risque
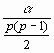 . Ce
test est dit "conservateur" car il devient plus difficile de mettre en
évidence une différence significative (l'hypothèse de
nullité est difficilement rejetée). La méthode de Bonferonni
est néanmoins très grossière, il faut donc
généralement l'éviter.
. Ce
test est dit "conservateur" car il devient plus difficile de mettre en
évidence une différence significative (l'hypothèse de
nullité est difficilement rejetée). La méthode de Bonferonni
est néanmoins très grossière, il faut donc
généralement l'éviter.
2.1.3 - Méthode de Newman-Keuls :
C'est certainement la méthode la plus utilisée. L'essentiel
du test de Newman-Keuls réside dans une approche séquentielle
ou l'on teste les comparaisons entre paires en choisissant la valeur critique
en fonction de l'étendue de la comparaison.
Pour simplifier l'exposé, nous admettrons que les moyennes sont
numérotées en fonction de leur ordre de grandeur : de
M1 (la plus petite) à MA (la plus grande).
Principe du test de Newman-Keuls : on sélectionne la comparaison entre
paire de moyennes correspondant à la plus grande différence.
(cette comparaison possède, donc, une étendue A). On teste
pour cette paire maximale, l'hypothèse de la nullité de la
différence des moyennes. Si l'on ne peut rejeter l'hypothèse
nulle, le test s'arrête là, car toutes les autres comparaisons
sont incluses dans celles-ci. Si l'on peut rejeter l'hypothèse nulle
alors on peut soumettre au test les deux comparaisons avec l'étendue
de (A-1), en prenant comme valeur critique la valeur obtenue dans la table
élaborée par Newman et Keuls pour une étendue de
(A-1).
Si l'on ne peut pas rejeter l'hypothèse nulle pour une comparaison,
alors on décide que toutes les comparaisons entre paires impliquées
par cette comparaison ne permettront pas non plus de rejeter l'hypothèse
nulle.
Si l'on peut rejeter l'hypothèse pour une comparaison alors on recommence
l'opération pour les moyennes séparées par une étendue
de (A-2), en choisissant la valeur critique dans la table de Newman-Keuls
pour une étendue de (A-2), et ce jusqu'à l'épuisement
de l'ensemble des paires.
Cette procédure séquentielle évite l'apparition de
décisions dissonantes : comme par exemple juger que la différence
entre M1 et M4 n'est pas significative, et admettre
que la différence entre M1 et M2 est significative.
Il faut se rappeler que les moyennes sont numérotées en fonction
de leur taille.
Signalons que la possibilité d'utiliser cette méthode lorsque
les effectifs sont inégaux est envisagée par Kramer.
2.1.4 - le test de Tukey :
Le test de Tukey emploie exactement la même procédure que celle
de Newman-Keuls mais la valeur critique choisie pour une étendue de
A moyennes (de la plus petite à la plus grande), reste utilisée
pour les autres comparaisons dont l'étendue est forcément moindre.
Le test est dit "conservateur" c'est-à-dire que l'hypothèse
de nullité est rejetée moins souvent qu'elle ne devrait (on
oublie de détecter des effets; on augmente l'erreur de type II,
b )
2.1.5 - le test de Duncan :
Ce test suit la procédure présentée dans le test de
Newman-Keuls mais utilise pour les valeurs critiques la table de Duncan.
Au même titre que le test de Newman-Keuls, il semble être un
test puissant.
Le choix de l'une ou de l'autre de ces méthodes reste d'ailleurs
très discutable (les "meilleures" semblent être celles de
Newman-Keuls et de Duncan), et la meilleure façon d'échapper
à ce choix est vraisemblablement d'éviter toute utilisation
des méthodes de comparaisons de moyennes deux à deux. Le plus
souvent, il ne se justifie d'ailleurs pas d'effectuer toutes les comparaisons
des moyennes deux à deux, le vrai problème étant de
réaliser certaines comparaisons particulières, telles que les
comparaisons d'une série de traitements avec un témoin. Ce
sont alors, selon les cas, les méthodes de Dunnet, de Gupta et Sobel,
de Scheffé qui doivent être utilisées.
2.1.6 - le test de Dunnet :
Il permet de comparer des groupes expérimentaux à un groupe
témoin (ou à un groupe contrôle).
On effectue dans ce cas, pour p populations, (p-1) comparaisons. l'erreur
globale de première espèce propre à la méthode
de la plus petite différence significative doit en conséquence
être réduite dans une moindre mesure que dans le cas
général, où le nombre de comparaisons à
réaliser est égal à p(p-1)/2. Des tables spéciales
ont été élaborées par Dunnet, pour traiter
correctement ce cas particulier.
Ces tables réunissent des valeurs
d1-a /2 qui doivent remplacer les valeurs
t1-a /2, de telle sorte que le risque
global de première espèce soit ramené au niveau de
a , pour l'ensemble des p-1 comparaisons. Ces
valeurs sont bien évidemment comprises entre celles correspondant
aux méthodes de la plus petite différence significative d'une
part et de Newman-Keuls d'autre part.
Toujours dans les conditions normales d'emploi de l'analyse de variance,
la différence entre la moyenne de l'échantillon témoin
et la moyenne de l'un quelconque des échantillons traités doit
être considérée comme significative lorsqu'elle égale
ou dépasse la valeur critique = d1-a
/2![]() .
.
Après avoir mis en évidence, par un test de Dunnet, les traitements
qui sont meilleurs que le témoin, il est possible d'enchaîner
un test de Newman-Keuls pour classer ces traitements entre eux.
2.1.7 - la recherche des moyennes les plus élevées : Gupta
et Sobel
Le but poursuivi est de délimiter le plus petit ensemble de moyennes
observées
![]() i
qui ait une probabilité élevée, par exemple
1-a , d'englober la population de moyenne
théorique maximum. Cet objectif peut être atteint, dans les
conditions habituelles de l'analyse de la variance, en réunissant
les valeurs
i
qui ait une probabilité élevée, par exemple
1-a , d'englober la population de moyenne
théorique maximum. Cet objectif peut être atteint, dans les
conditions habituelles de l'analyse de la variance, en réunissant
les valeurs
![]() i
qui sont telles que :
i
qui sont telles que :
![]() i
³
i
³
![]() max -
d1-a
max -
d1-a
![]()
où
![]() max désigne
la moyenne la plus élevée, CMr le carré moyen
résiduel et n le nombre d'observations intervenant dans chacune des
moyennes. Quand au facteur d1-a , il
représente les valeurs déjà utilisées dans le
test de Dunnet, mais relatives ici à un test unilatéral. La
méthode présentée ici revient donc à effectuer
un test unilatéral de comparaison de p-1 moyennes observées
avec une moyenne témoin, la valeur maximum servant de témoin.
max désigne
la moyenne la plus élevée, CMr le carré moyen
résiduel et n le nombre d'observations intervenant dans chacune des
moyennes. Quand au facteur d1-a , il
représente les valeurs déjà utilisées dans le
test de Dunnet, mais relatives ici à un test unilatéral. La
méthode présentée ici revient donc à effectuer
un test unilatéral de comparaison de p-1 moyennes observées
avec une moyenne témoin, la valeur maximum servant de témoin.
2.1.8 - le test de Scheffé :
La méthode de Scheffé repose sur le test de contrastes. On
appelle contraste une somme pondérée de moyennes :
C = c1m1 + c2m2 + ... +
ckmk
avec S ci = 0
et S |ci| = 2 (afin
d'homogénéiser les coefficients)
Exemples :
1, -1, 0, 0 pour comparer m1 avec m2
1, 0; -1; 0 pour comparer m1 et m3
1/2, 1/2, -1/2, -1/2 pour comparer m1 et m2 avec
m3 et m4
le contraste est jugé significatif si la valeur absolue de C est
supérieure à : S =
![]()
p étant le nombre de niveaux de la variable indépendante ; Fc étant la valeur critique de F avec p-1 et n-p degrés de liberté, pour le seuil a déterminé. Cette valeur est lue dans la table de Fisher - Snedecor. ni étant l'effectif du groupe du niveau i ; CMa : étant les carrés moyens du facteur a à p niveaux.
2.2 L'analyse de variances à deux facteurs de variabilité
:
Les expériences factorielles doubles, ou plus généralement
multiples, sont importantes pour les raisons suivantes :
Nous avons vu que l'analyse de variance à un critère de
classification a notamment pour principe de diviser la variation totale en
deux composantes : l'une factorielle, l'autre résiduelle. Cette
façon de procéder peut être étendue à deux
critères de classification, la variation totale étant alors
divisée en plus de deux composantes : l'une résiduelle
également, et les autres liées aux deux critères de
classification.
Les deux facteurs considérés peuvent être placés
sur le même pied ou subordonnés l'un à l'autre. les
modèles de l'analyse de variance correspondant au premier cas sont
dits croisés, ceux qui correspondent au deuxième cas sont dits
hiérarchisés (ou emboîtés). Dans chaque cas, on
doit distinguer aussi un modèle fixe, un modèle aléatoire
et un modèle mixte selon que les deux critères de classification
sont fixes, aléatoires ou l'un fixe et l'autre aléatoire.
Considérons pq populations dans chacune desquelles est
prélevée un échantillon d'effectif n et
désignons par xijk les différentes valeurs
observées, l'indice i servant à distinguer p variantes (ou
niveaux) d'un premier critère de classification (i = 1, …, p),
l'indice j permettant de distinguer q variantes d'un deuxième
critère de classification (j + 1, …, q) et k désignant,
pour chaque échantillon, les numéros d'ordre des différentes
observations (k = 1, …, n).
A partir de ces données, on peut calculer une moyenne par
échantillon :
![]() ij. =
ij. =
![]()
une moyenne par variante (par facteur) de chacun des deux critères de classification :
![]() i.. =
i.. =
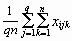 =
= ![]() et
et ![]() .j. =
.j. =
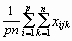 =
= ![]()
et une moyenne générale :
![]() … =
… =
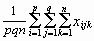 =
= 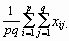 =
= ![]() =
= ![]()
En se basant sur ces définitions, on peut diviser les écarts par rapport à la moyenne générale en deux, puis en quatre composantes, et écrire le modèle observé :
xijk -
![]() … =
(
… =
(![]() ij. -
ij. -
![]() …) +
(xijk -
…) +
(xijk -
![]() ij.)
ij.)
= (![]() i.. -
i.. -
![]() …) +
(
…) +
(![]() .j. -
.j. -
![]() …) +
(
…) +
(![]() ij. -
ij. -
![]() .i.. -
.i.. -
![]() .j. +
.j. +
![]() …) +
(xijk -
…) +
(xijk -
![]() ij.)
ij.)
La première décomposition est identique à celle qui a été réalisée au cours de l'analyse de la variance à un critère de classification. La seconde décomposition distingue en plus du terme résiduel, deux termes mesurant les différences entre la moyenne générale et les moyennes relatives aux différentes variantes des deux critères de classification, et enfin, un terme d'interaction :
![]() ij. -
ij. -
![]() .i.. -
.i.. -
![]() .j. +
.j. +
![]() …
…
Ces termes d'interaction sont nuls lorsque les différences liées à l'action d'un des deux facteurs contrôlés sont indépendantes de l'action de l'autre.
Xijk - m.. = (mi. - m..) + (m.j - m..) +
(mij - mi. - m.j + m..) + (Xijk
- mij)
ou Xijk = m.. + a i +
b j + g
ij + e ijk
avec : Xijk : représente la variable dépendante
;m.. : la moyenne générale de la population parentale, elle
est estimée par ![]() ...,
la moyenne de l'ensemble des échantillons ; mi. les moyennes
théoriques relatives aux différents niveaux du facteur a
(estimées par les moyennes
...,
la moyenne de l'ensemble des échantillons ; mi. les moyennes
théoriques relatives aux différents niveaux du facteur a
(estimées par les moyennes
![]() i.. des
échantillons) ; m.j les moyennes théoriques relatives
aux différents niveaux du facteur b (estimées par les moyennes
i.. des
échantillons) ; m.j les moyennes théoriques relatives
aux différents niveaux du facteur b (estimées par les moyennes
![]() .j. des
échantillons) ; a i : les
écarts factoriels, a i =
mi. - m.., mesurant les différences théoriques entre
les moyennes des différents niveaux et la moyenne générale
pour le facteur a ; b j : les écarts
factoriels, b j = m.j -
m.., mesurant les différences théoriques entre les moyennes
des différents niveaux et la moyenne générale pour le
facteur b ; Les quantités a i
et b j sont souvent appelées
effets du facteur contrôlé ou effets principaux ;
g ij sont des valeurs théoriques
des interactions ; e ijk : les écarts
résiduels (e ijk =
Xijk - mij). e
ijk correspond à l'erreur expérimentale de l'observation
Xijk. Ces écarts résiduels sont normaux,
indépendants de moyenne nulle et d'écart-type
s .
.j. des
échantillons) ; a i : les
écarts factoriels, a i =
mi. - m.., mesurant les différences théoriques entre
les moyennes des différents niveaux et la moyenne générale
pour le facteur a ; b j : les écarts
factoriels, b j = m.j -
m.., mesurant les différences théoriques entre les moyennes
des différents niveaux et la moyenne générale pour le
facteur b ; Les quantités a i
et b j sont souvent appelées
effets du facteur contrôlé ou effets principaux ;
g ij sont des valeurs théoriques
des interactions ; e ijk : les écarts
résiduels (e ijk =
Xijk - mij). e
ijk correspond à l'erreur expérimentale de l'observation
Xijk. Ces écarts résiduels sont normaux,
indépendants de moyenne nulle et d'écart-type
s .
Ce modèle théorique peut faire l'objet de trois hypothèses
nulles différentes.
L'une est relative à l'absence d'action du premier facteur :
Ho : a 1 =
a 2 = ... =
a P = 0 ou m1. =
m2. = ... = mp.
La seconde est relative à l'absence d'action du deuxième facteur
:
H'o : b 1 =
b 2 = ... =
b q = 0 ou m.1 =
m.2 = ... = m.q
La troisième concerne l'absence d'interactions :
H''o : g 11 =
g 12 = ... =
g pq = 0 ou mij -
m.j = a i pour tout i et
tout j
ou encore mij - mi. = b
j pour tout i et tout j.
Les calculs des sommes des carrés des écarts puis des carrés moyens permettent de tester la validité de ces hypothèses. Les différentes comparaisons des carrés moyens sont résumés dans le tableau suivant.
Source de variabilité
|
ddl
|
carrés moyens
|
F
|
Facteur a
|
p-1
|
CMa = SCEa / (p-1)
|
Fa = CMa / CMr
|
Facteur b
|
q-1
|
CMb = SCEb / (q-1)
|
Fb = CMb / CMr
|
Interaction
|
(p-1)(q-1)
|
CMab = SCEab / (p-1)(q-1)
|
Fab = CMab / CMr
|
Variation résiduelle
|
pq(n-1)
|
CMr = SCEt / pq(n-1)
|
|
Totaux
|
pqn-1
|
CMt = SCEt / (pqn-1)
|
Ce tableau est valable si les différents groupes ont des effectifs égaux. C'est d'ailleurs dans ce cas que la puissance de l'analyse de variance est maximale. L'expérimentateur a donc tout intérêt de prendre un même nombre d'unités expérimentales pour l'ensemble des groupes.
Remarques :
Dans le chapitre précédent (ANOVA à un facteur), nous
avons expliqué les différences entre facteurs fixes et facteurs
aléatoires. Trois modèles peuvent être rencontrés
:
Puissance de l'analyse variance à deux facteurs :
Pour chaque facteur, le paramètre f prend
la valeur :
f =
![]()
avec p' = nombre de groupes par facteur
Pour l'effet interaction :
f =
![]()
A partir de f , la puissance du test est connue en consultant les graphes de Hartley et Pearson.
Cas particuliers :
Quand on compare la moyenne d'un paramètre dans plusieurs groupes,
il est crucial de pouvoir disposer de groupes comparables, mais aussi de
groupes les plus homogènes possible afin d'obtenir une puissance
élevée pour la comparaison. Il est parfois des situations
expérimentales où l'on connaît par avance certains facteurs
susceptibles de nuire à une telle homogénéité.
Différents plans d'expérience ont donc été
conçus afin d'éliminer les effets des sources d'erreur.
Si on cherche à réduire les effets d'une seule source d'erreur,
on utilisera la méthode des blocs (complets si possibles). Pour deux
sources d'erreurs, ce sera la méthode des carrés latins, et
pour trois, quatre ou cinq sources d'erreurs, le plan d'expérience
utilisé sera un plan carré graeco-latin.
- La méthode des blocs :
On désigne par blocs des ensembles dans lesquels sont regroupées
les unités expérimentales de telle sorte qu’elles soient
aussi semblables que possible à l’intérieur de chaque
bloc.
On peut s’attendre ainsi à ce que l’erreur expérimentale
soit moindre que pour un même nombre d’unités
aléatoirement situées à l’intérieur de la
totalité de l’espace expérimental.
Les blocs sont généralement déterminés pour tenir
compte, outre les causes contrôlables définies par les facteurs
étudiés, d’autres causes qu’il peut être difficile,
voire impossible, de maintenir constantes sur la totalité des unités
expérimentales de l’expérience.
Les variations entre les blocs sont alors éliminés lorsque
l’on compare les effets des facteurs.
Cette méthode peut être comparée à une analyse
de variance à deux facteurs croisés. Le premier facteur étant
le facteur étudié, le second se rapportant aux blocs.
Si toutes les situations sont représentées dans l'expérience
réalisée, on dit qu'on utilise un plan à blocs complets;
si ce n'est pas le cas, c'est un plan à blocs incomplets.
Exemple : si on compare le rendement de quatre variétés de maïs en les semant sur un lot de parcelle (six par exemple); les différences de fertilité de ces dernières vont introduire une variabilité parasite, nuisible pour la comparaison. L'idéal serait de découper chaque parcelle en quatre, de répartir aléatoirement chaque variété dans chaque quart pour comparer la productivité de chaque espèce de maïs au sein de chaque parcelle, et finalement résumer ces six comparaisons en une seule conclusion.
La figure suivante montre l'arrangement aléatoire des 4 variétés de maïs dans 6 parcelles.
Parcelle 1
(bloc 1) |
Rendement
Maïs 2 |
Rendement
Maïs 1 |
Rendement
Maïs 4 |
Rendement
Maïs 3 |
Parcelle 2
(bloc 2) |
Rendement
Maïs 1 |
Rendement
Maïs 3 |
Rendement
Maïs 2 |
Rendement
Maïs 4 |
Parcelle 3
(bloc 3) |
Rendement
Maïs 2 |
Rendement
Maïs 3 |
Rendement
Maïs 1 |
Rendement
Maïs 4 |
Parcelle 4
(bloc 4) |
Rendement
Maïs 4 |
Rendement
Maïs 2 |
Rendement
Maïs 3 |
Rendement
Maïs 1 |
Parcelle 5
(bloc 5) |
Rendement
Maïs 3 |
Rendement
Maïs 4 |
Rendement
Maïs 1 |
Rendement
Maïs 2 |
Parcelle 6
(bloc 6) |
Rendement
Maïs 1 |
Rendement
Maïs 4 |
Rendement
Maïs 2 |
Rendement
Maïs 3 |
Une analyse de variance à deux facteurs (le premier facteur correspond au rendement; le second à l'effet bloc) pourra nous dire si, après élimination des effets de bloc, il existe une différence significative entre les variétés de maïs.
- La méthode des carrés latins
Le carré latin est un dispositif qui permet de contrôler
l'hétérogénéité du matériel
expérimental dans deux directions.
Dans certaines expériences, il arrive qu'une série de k traitements
soit donnée à des sujets à des moments différents
(ou à des endroits différents du corps s'il s'agit de
crèmes), et que l'ordre (ou le lieu d'application) dans lequel est
donnée la séquence soit potentiellement important. Il est alors
indispensable de tenir compte dans l'analyse d'un effet "ordre (ou lieu)
d'administration" et faire attention à ce que chaque traitement soit
donné de façon équilibrée en
1ère , 2ème, ..., kème
position. L'utilisation des carrés latins répond à cet
impératif.
Prenons l'exemple de 4 traitements donnés à 4 moments
différents de la journée. Les sources d'erreur sont :
- les moments de la journée
- l'ordre d'administration
Dans la figure suivante sont représentés par des lettres les 4 traitements. Les lignes du tableau représente les moments; les colonnes, l'ordre.
A
|
B
|
C
|
D
|
B
|
C
|
D
|
A
|
C
|
D
|
A
|
B
|
D
|
A
|
B
|
C
|
Chaque traitement doit apparaître une fois dans chaque ligne et dans
chaque colonne. Dans un carré latin, le nombre de lignes doit être
égal au nombre de colonnes. Ainsi le carré latin sera toujours
de type 3 x 3 ou 4 x 4 …
Pour un carré latin 3 x 3, il y a donc 12 configurations possibles;
pour un carré latin 4 x 4, 576; pour un carré latin 5 x 5,
161.280 combinaisons différentes …
La méthode des carrés latins est assimilée à
une analyse de variance à trois facteurs. En effet, le premier facteur
est le facteur traitement; les deux autres correspondent aux sources d'erreur
(facteur ligne et facteur colonne).
En résumé :
tests paramétriques |
tests non-paramétriques |
|||
Echantillons
Appariés |
2 v.a. / 1 pop
Student |
k v.a. / 1 pop
ANOVA |
2 v.a. / 1 pop
Wilcoxon |
k v.a. / 1 pop
Friedman |
Echantillons
Indépendants |
1 v.a. / 2 s.pop
Student |
1 v.a. / k s.pop
ANOVA |
1 v.a. / 2 s.pop
Mann-Whitney |
k v.a. / 2 s.pop
Kruskall-Wallis |
Echantillons
Appariés |
k v.a. / 2 s.pop
T² Hotelling |
k v.a. / k s.pop
MANOVA |
||
Echantillons
Indépendants |
k v.a. / 2 s.pop
T² Hotelling |
k v.a. / k s.pop
MANOVA |
||
La droite d'une régression linéaire peut s'écrire :
Y = aX + b + e
avec Y : la variable à expliquer ou la variable dépendante,
X : la variable estimée ou la variable indépendante et
e : les erreurs également appelées
les résidus qui correspondent aux différences entre les valeurs
réelles de la variable dépendante Y et son estimation
Yi.
Pour valider ce modèle, il faut vérifier au préalable les quatre conditions suivantes :
Les tests ou graphiques couramment utilisés sont :
par un histogramme
par la droite de Henry : pour valider cette hypothèse, il faut que les points forment une droite pratiquement parfaite.
par l'analyse des résidus en étudiant le graphe Yi - Yestimé = f(X) (équivalent à tracer les résidus (Yi - Yestimé) en fonction de Yestimé car Yestimé est également une fonction linéaire de X).
Si le modèle choisi est adéquat, les résidus sont
distribués uniformément sur une bande horizontale du graphique
entre les valeurs de -2 et de +2 : ce qui correspond à 95% de
l'échantillon (référence à +1.96 et -1.96 de
la distribution normale).
Ce graphe des résidus permet de confirmer également
l'hypothèse 3. Le graphique peut prendre des allures différentes.
Les trois figures ci-dessous montrent que:
1°) la variance s ² n'est pas
constante. Dans ce cas, il est nécessaire d'effectuer une transformation
des données Yi avant d'effectuer l'analyse de régression.
2°) le modèle choisi est inadéquat (le modèle est
linéaire, mais on a par exemple omis le terme constant alors que celui-ci
est nécessaire)
3°) le modèle choisi est inadéquat (tendance parabolique)
Remarques :
L'équation de la régression est : Y = X1 + X2 + X3 + ... + Xj + e
Condition de validité :
Une régression multiple doit le plus possible s'approcher de ces
conditions
F =
![]()
p : nombre de variables explicatives , n : nombre de valeurs de chaque variable
Si F calculé est supérieur à F lu dans la table de Fisher-Snedecor pour n 1 = p et n 2 = n-p-1 degrés de liberté, le coefficient de corrélation multiple est significatif pour a donné.
- Significativité de chaque régresseur :
R peut se révéler significatif alors que l'équation de régression contient un ou plusieurs variables explicatives inutiles. Le test des coefficients de corrélation partielle permet de détecter les variables qui peuvent être rejetées. Un coefficient de corrélation partielle se teste comme un coefficient de corrélation simple avec n-p-1 degrés de liberté.
C'est une technique descriptive qui permet de faire la synthèse de
l'information contenue dans un grand nombre de variables.
But de l'ACP :
Il est aisé de représenter les observations d'une variable
(sur une droite), de deux variables (dans un plan), de trois variables (en
faisant de la géométrie dans l'espace) mais l'étude
devient impossible lorsque le nombre de variables est supérieur à
trois.
Le but de la méthode est la réduction des dimensions de l'espace
de représentation des données en projetant le nuage de points
dans un ou plusieurs graphiques plan, en essayant de limiter la perte
d'informations au cours de cette réduction. Les "composantes principales"
seront des nouvelles variables, indépendantes, combinaisons
linéaires des variables initiales, possédant une variance
maximum.
Cette technique ne s'applique qu'à des variables quantitatives.
Pour des variables qualitatives, on utilisera plutôt les analyses des
correspondances multiples.
La première étape d'une analyse en composantes principales
est de centrer et réduire l'ensemble des variables. En effet, dans
la plupart des cas, les données à analyser sont
hétérogènes tant du point de vue des ordres de grandeur
que des échelles de utilisées.
Le centrage consiste à soustraire à chaque valeur la moyenne
de la variable correspondante et la réduction s'effectue en divisant
chacune des valeurs du tableau par l'écart-type correspondant. Ce
procédé permet de donner la même importance à
toutes les variables quelles que soient les échelles de mesure dans
lesquelles elles sont exprimées. Cette opération est indispensable
lorsqu'on est en face à des unités de mesure
différentes.
Les ACP fournissent généralement dans un premier temps la matrice
de corrélation que l'on est pas obligé d'examiner car il y
a souvent beaucoup de données (pour 10 variables étudiées,
il y aura 100 coefficients de corrélation).
La deuxième étape est l'examen des pourcentages d'inertie fournis
avec les valeurs propres (ces dernières peuvent être utiles
essentiellement pour calculer les coordonnées de nouvelles composantes
principales). C'est une étape importante car elle permet de savoir
sur quels axes se trouve le maximum d'informations et de choisir le nombre
d'axes à étudier.
Le pourcentage d'inertie d'un axe est synonyme de pourcentage d'information
totale retrouvée sur cet axe. Il est évident qu'à la
suite de chacune des projections du nuage de points sur les différents
axes, le pourcentage d'information va dans le sens d'une diminution.
Au pourcentage d'inertie est associé le pourcentage d'inertie
cumulée. C'est ce paramètre qu'il faut tenir compte pour le
choix du nombre d'axes. Par exemple, sur les trois premiers axes il y a 82%
d'inertie cumulée (50% sur l'axe 1, 20% sur l'axe 2 et 12% sur l'axe
3) soit 82% des informations se retrouvent sur les axes 1, 2 et 3.
Généralement, on ne tient compte que des axes regroupant 80%
d'information totale. Dans cet exemple là, on étudiera les
plans (1,2) appelé aussi plan principal, (1,3) et (2,3). Il faudra
alors rester prudent lors des interprétations car nous ne sommes pas
en présence de toutes les informations sur les axes choisis.
Les logiciels spécifient ensuite pour chaque variable et pour chaque individu sa coordonnée, sa qualité de représentation et sa contribution par rapport à chacun des axes factoriels.
* les variables :
Exemple numérique : supposons que l'on relève les coordonnées et qualités de représentation suivantes pour une variable V dans une analyse relative à un espace de 4 dimensions :
| variable V | coordonnée | qualité de rep. |
axe 1 |
0.71 |
0.50 |
Le premier axe, avec une corrélation de 0.71 rend compte de 50% de
la dispersion de la variable V, le deuxième axe, avec une
corrélation négative de -0.50 concentre 25%, le troisième
5% et le quatrième 20%. Ainsi, la moitié de l'information relative
à la variable V est concentrée sur le premier axe, les axes
2 et 4 rendant compte ensemble de la majeure partie de l'autre
moitié.
La qualité de représentation d'une variable par un groupe d'axe
s'obtient en additionnant les valeurs relatives à chacun des axes.
Ainsi, le premier plan factoriel concentre 75% de l'information relative
à la variable V dans l'exemple ci-dessous.
- La contribution d'une variable à un axe :
La somme des carrés des coordonnées de l'ensemble des variables
sur l'axe est égale à la valeur propre associée à
l'axe. La contribution de chaque variable s'obtient en effectuant le rapport
entre le carré de sa coordonnée et la valeur propre. Les
contributions mesurent donc les rôles relatifs joués par chacune
des variables dans la formation de l'axe, et l'addition de toutes les
contributions vaut 1.
En règle générale, on examine les contributions à
l'élaboration des axes : pour p variables, seules on
considérera sur un axe k les variables possédant des
contributions supérieures à 1/p (ce qui signifie que
ce sont essentiellement ces variables qui auront contribué à
la formation de cet axe k).
* Les individus :
les contributions des individus aux axes factoriels :
De la même manière que pour les variables, les individus contribuent
différemment à la formation de chaque axe factoriel. Ces valeurs
sont surtout utiles pour détecter des individus aberrants : par exemple,
un individu avec une contribution de 82.4% sur un axe k peut être
considérer comme aberrant. Cela a pour conséquence de fausser
l'étude et il serait alors conseiller de faire une deuxième
analyse en mettant ces individus en éléments supplémentaires.
La qualité de représentation des individus sur les axes factoriels
:
Elle est mesurée par le cosinus carré de l'angle
a formé par le vecteur GC avec l'axe
k.
Plus la valeur sera proche de l'unité, meilleure sera la
représentation de l'individu sur un axe.
Ci-dessous, je donne les valeurs de la loi de Student pour un risque d'erreur a = 5% et a = 1%. Pour un échantillon de taille n, il faudra prendre n-1 degrés de liberté.
ddl |
a = 0.05 |
a = 0.01 |
ddl |
a = 0.05 |
a = 0.01 |
|
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
12.710 4.303 3.182 2.776 2.571 2.447 2.365 2.306 2.262 2.228 2.201 2.179 2.160 2.145 2.131 2.120 2.110 2.101 2.093 2.086 2.080 2.074 2.069 2.064 2.060 |
63.660 9.925 5.841 4.604 4.032 3.707 3.499 3.355 3.250 3.169 3.106 3.055 3.012 2.977 2.947 2.921 2.898 2.878 2.861 2.845 2.831 2.819 2.807 2.797 2.787 |
26 27 28 29 30 32 34 36 38 40 50 60 70 80 90 100 200 300 400 500 600 700 800 900 1000 ¥ |
2.056 2.052 2.048 2.045 2.042 2.037 2.032 2.028 2.024 2.021 2.009 2.000 1.994 1.990 1.987 1.984 1.972 1.968 1.966 1.965 1.964 1.963 1.963 1.963 1.962 1.960 |
2.779 2.771 2.763 2.756 2.750 2.738 2.728 2.719 2.712 2.704 2.678 2.660 2.648 2.639 2.632 2.626 2.601 2.592 2.588 2.586 2.584 2.583 2.582 2.581 2.581 2.576 |
Si r calculé est supérieur à r lu dans la table, on conclut qu'il existe une corrélation linéaire significative, avec un risque a fixé.
r se lit en fonction du degré de liberté ; ddl = n - p -1 où
n : nombre de couples ; p : nombre de variables explicatives
(une seule dans le cas d'une corrélation simple)
| ddl | a = 0.05 | a = 0.01 | ddl | a = 0.05 | a = 0.01 | |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
0.997 0.950 0.878 0.811 0.755 0.707 0.666 0.632 0.602 0.576 0.553 0.532 0.514 0.497 0.482 0.468 0.456 0.444 0.433 0.423 0.413 0.404 0.396 0.388 0.381 0.374 0.367 0.361 0.355 0.349 0.344 0.339 0.334 0.329 0.325 0.320 0.316 0.312 0.308 0.304 0.301 0.297 0.294 0.291 0.288 0.285 0.282 0.279 0.276 0.273 |
1.0000 0.990 0.959 0.917 0.875 0.834 0.798 0.765 0.735 0.708 0.684 0.661 0.641 0.623 0.606 0.590 0.575 0.561 0.549 0.537 0.526 0.515 0.506 0.496 0.487 0.479 0.471 0.463 0.456 0.449 0.442 0.436 0.430 0.424 0.418 0.413 0.408 0.403 0.398 0.393 0.389 0.384 0.380 0.376 0.372 0.368 0.365 0.361 0.358 0.354 |
52 54 56 58 60 62 64 66 68 70 72 74 76 78 80 82 84 86 88 90 92 94 96 98 100 105 110 115 120 125 130 135 140 145 150 160 170 180 190 200 250 300 350 400 450 500 600 700 800 900 1000 |
0.268 0.263 0.259 0.254 0.250 0.246 0.242 0.239 0.235 0.232 0.229 0.226 0.223 0.220 0.217 0.215 0.212 0.210 0.207 0.205 0.203 0.201 0.199 0.197 0.195 0.190 0.186 0.182 0.178 0.174 0.171 0.168 0.165 0.162 0.159 0.154 0.150 0.145 0.142 0.138 0.124 0.113 0.105 0.098 0.092 0.088 0.080 0.074 0.069 0.065 0.062 |
0.348 0.341 0.336 0.330 0.325 0.320 0.315 0.310 0.306 0.302 0.298 0.294 0.290 0.286 0.283 0.280 0.276 0.273 0.270 0.267 0.264 0.262 0.259 0.256 0.254 0.248 0.242 0.237 0.232 0.228 0.223 0.219 0.215 0.212 0.208 0.202 0.196 0.190 0.185 0.181 0.162 0.148 0.137 0.128 0.121 0.115 0.105 0.097 0.091 0.086 0.081 |
La table fournit les valeurs critiques au-delà desquelles les coefficients de corrélation de Spearman obtenus sont significatifs. Pour des échantillons de taille n, on prendra n comme degrés de liberté.
n
|
a = 0.05
|
a = 0.01
|
n
|
a = 0.05
|
a = 0.01
|
|
| 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
1.000 .886 .786 .738 .700 .648 .618 .587 .560 .538 .521 .503 .485 .472 .460 .447 .435 .425 .415 .406 .398 .390 .382 .375 .368 .362 |
1.000 .929 .881 .833 .794 .755 .727 .703 .675 .654 .635 .615 .600 .584 .570 .556 .544 .532 .521 .511 .501 .491 .483 .475 .467 |
31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 60 70 80 90 100 |
.356 .350 .345 .340 .335 .330 .325 .321 .317 .313 .309 .305 .301 .298 .294 .291 .288 .285 .282 .279 .255 .235 .220 .207 .197 |
.459 .452 .446 .439 .433 .427 .421 .415 .410 .405 .400 .395 .391 .386 .382 .378 .374 .370 .366 .363 .331 .307 .287 .271 .257 |
Calcul de
![]() :
:
A = 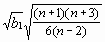 B =
B =
![]()
C = 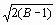 - 1 D =
- 1 D = ![]()
E = ![]() F =
F = ![]()
![]() =
= ![]()
avec b1 : estimation du coefficient d'asymétrie de Pearson b 1
![]() =
=
![]()
g1 =
![]() =
= ![]() : estimation du coefficient d'asymétrie de Fisher
g 1
: estimation du coefficient d'asymétrie de Fisher
g 1
k3 : estimation de m 3 moment de la moyenne d'ordre 3
k3 =
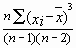 =
= 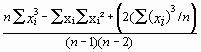
Calcul de
![]() :
: ![]() =
= 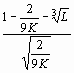
H = 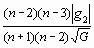 G =
G = ![]()
J = 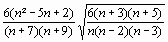 K =
K = ![]()
L = 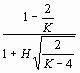
avec g2 estimation du coefficient d'aplatissement de Pearson b 2
g2 =
![]() =
= ![]()
k4 : estimation de m 4 moment de la moyenne d'ordre 4
k4 =
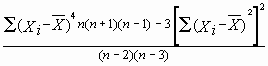
= ![]()
(en gras les livres conseillés)