Les Précurseurs de la Biomécanique

D'après son objet, la biomécanique est une mécanique appliquée, ses méthodes de recherche sont dérivées de celles de la mécanique, mais la biomécanique ne s'est pas développée au sein de la mécanique : elle est le produit d'autres disciplines scientifiques telles que l'anatomie, la physiologie, les sciences du sport telles que l'on peut les concevoir en STAPS, l'ergonomie...
La biomécanique s'est développée en tant que science limitrophe.

Quelques Repères Historiques

XV° siècle

• Léonard DE VINCI (1452-1519) s'est intéressé aux mouvements du corps sous l'angle des lois de la mécanique.

XVII° siècle

• Giovanni Alfonso BORELLI  (1608-1679) médecin et mathématicien italien, est le premier à déterminer expérimentalement la position centre de gravité (Cf. loi de Borelli, Weber, Fick en kinésithérapie). Dés 1679, il défend l'idée que les muscles constituent un ensemble de leviers obéissant aux lois mathématiques.

XIX° siècle

• Eduard Friedrich WEBER (1806-1891), médecin physiologiste allemand, spécialiste du système musculaire, étudie expérimentalement la marche ("Une mécanique de l'appareil humain de la marche" 1836). Sa théorie d'un mouvement pendulaire pur, fut réfutée par la suite.
• Jules-Etienne MAREY (1830-1904) médecin physiologiste français, mérite notre attention.
  Dès 1880, il met au point la chronophotographie (A) et un générateur dynamographique à base pneumatique (B). Ce sont là, les prémices d'une approche cinématique et dynamique du mouvement humain. Il collabore étroitement avec G. Demeny
• Georges DEMENY (1850-1917), photographe, précurseur du cinéma, assistant de J-E. Marey, il invente le phonoscope et un chronophotographe dont il vend les droits à la société Gaumont.
• BERNSTEIN perfectionna la chrono-photographie
• Le XIX° voit apparaître une prévalence de l'orthopédie, de la physiologie du travail dans l'industrie (Ergonomie).
  La rénovation des Jeux Olympiques augmente l'intérêt porté à l'amélioration des techniques sportives et favorise l'utilisation rationnelle des lois mécaniques appliquées aux APS pour en expliquer les grands principes.
  Fin XIX°s., la mécanisation de la production industrielle et l'automatisation des chaînes de montage, entre autres, a vue croître l'intérêt pour la biomécanique
  

XX° siècle

• Début XX°s, inspirés des travaux de Marey, Christian Wilhelm BRAUNE (1831-1892) et Otto FISCHER (1861-1917) étudient la  marche et proposent une nouvelle méthode de détermination du centre de gravité.
• En URSS : mise au point d'un grand nombre de dynamographes spéciaux destinés à la mesure biologique des performances sportives (ABALAKOV)
• 1931 : 1^ier cycle de conférences "Biomécanique des exercices physiques" à l'Institut de Culture Physique de LENINGRAD. On y aborde la cinésiologie (terme américain) ou l'analyse du mouvement (terme français) mais l'objet d'étude est encore discuté.
• A partir de la 2° guerre mondiale : la biomécanique est considérée comme discipline scientifique indépendante.
• 1960 : 1^ière conférence internationale relative aux questions fondamentales de la biomécanique des gestes sportifs à Leipzig, Allemagne.
  

Biomécanique Instrumentale

Principaux Outils de Mesure

Les méthodes de mesure et de traitement des données sont à la base de tout travail scientifique

Anthropométrie biomécanique

Elle comporte les mesures classiques :

• Poids, taille, taille assise, pourcentage de graisse (méthode des plis cutanés), densité, flottabilité...
• Les nouvelles méthodes d'investigation utilisent des méthodes non-invasives (scanner, IRM...) et permettent d'analyser de minces tranches de toutes les parties du corps humain et de réaliser, sur ordinateur, des reconstructions 3D des différentes structures internes du corps : os, articulations, muscles, ligaments.
  En dépit, de quelques limitations, ces nouvelles méthodes permettent une étude quantitative des dimensions du corps humain, ce qui est la condition première à la modélisation du corps. La spectro-RMN donne la densité de différents protons (H, P, Ca, Mg...) à l'intérieur de l'organisme, il est ainsi possible de voir évoluer en temps réel un pH ou un métabolisme à l'intérieur d'un muscle et ce sans aucun prélèvement, cette méthode encore au stade du laboratoire est promise à un bel avenir, bien que l'analyse en temps réel d'une pratique physique ne semble aujourd'hui que peu envisageable.

Électromyographie (EMG)

Contrairement à la plus part des méthodes électroniques qui donnent des informations sur les propriétés mécaniques et les sorties du système musculo-squelettique, l'EMG représente ou indique l'entrée neurale du muscle. En tant que paramètre de contrôle, l'EMG est de première importance pour la modélisation du système neuro-musculo-squelettique dynamique (HATZE, 1981).
Cependant, un point particulier est à prendre en considération : le signal électrique EMG est un indicateur indirect de la tension ou de la force musculaire. De nombreux efforts scientifiques ont été consacrés aux relations quantitatives entre le signal EMG et la sortie mécanique du muscle. Il apparaît qu'après traitement, l'EMG peut, dans certaines conditions, être corrélé mais n'est qu'une mesure indirecte de la force musculaire (SPAEPEN et al., 1987). La situation est encore plus incertaine pour interpréter l'EMG dans les cas dynamiques.

Goniomètres

EN CONSTRUCTION

Jauges Électriques d'Extensométrie (ou Jauge de contrainte)

Théorie : La transformation d'une grandeur physique en information électrique est intéressante en raison de ses qualités de précision et de fidélité et de la souplesse d'emploi et de mesure.
Les techniques de fabrication actuelles utilisent les procédés des circuits imprimés (photographie et attaque du métal), elle permet d'obtenir des jauges dites pelliculaires très plates avec un support de 20 à 30 microns en résine époxy à partir d'une feuille de métal de 2 microns.

Sous sa forme la plus simple, une jauge est constituée par un fil très fin collé sur une feuille très mince, le fil est disposé comme le montre le schéma suivant, c'est à dire que les brins de fil sont principalement alignés suivant une direction unique D à l'exception des boucles de raccordement entre les brins successifs. Deux fils plus épais servent à souder les sorties à des câbles de liaison aux instruments.

Schéma d'une jauge d'extensométrie

D : la direction principale des fils électriques

On admet, en première approximation, que le fil subit les mêmes modifications que la surface sur laquelle elle est collée. La jauge est donc collée, fils parallèles à la direction dont on désire connaître l'allongement ou étudier les déformations.

Principes de fonctionnement : La théorie communément admise est celle qui considère que le fil subit les mêmes déformations que s'il était tendu par ses extrémités. Un fil fin que l'on soumet à une traction, dans les limites de son domaine élastique, s'allonge sous l'effet de la charge, cependant que sa section diminue. Si l est l'allongement relatif, le diamètre subit une diminution relative. Sachant que la résistance d'un fil conducteur est :

R = p.l/s
où R : la résistance (Ohm), p : la résistivité (Ohm x mètre),
l : la longueur (m), s : la section du fil (m²)

Par exemple, à un étirement de la jauge dans la direction D, correspond une augmentation de l, une diminution de s et donc une variation de la résistance R

δR/R = K . δl/l
K : constante relative au matériau considéré

La mesure de variation de résistance est donc liée à l'allongement relatif ou déformation longitudinale de la pièce sur laquelle elle est collée. Ce sont les règles de la R.D.M. qui servent à grouper les jauges en vue de la détection d'une composante particulière de la déformation du corps d'épreuve. Un montage particulier (en pont de Wheatstone) permet d'ajouter ou de retrancher entre eux les effets séparés de deux jauges. C'est ainsi que sont éliminés les phénomènes parasites au profit d'une grandeur majorante. La tension de sortie (δV) peut être exploitée directement à l'aide d'un galvanomètre ou autre système d'acquisition.

Capteurs de Forces à jauges

Généralités : Un capteur est un instrument destiné à transformer une grandeur physique quelconque en une grandeur électrique, en vue d'une mesure ou d'une action sur un dispositif régulateur.

Cette transformation en information électrique est intéressante en raison des qualités (précision, fidélité) et de la souplesse d'emploi des dispositifs électromécaniques ou électroniques. Les applications des capteurs sont très nombreuses : pesée industrielle, mesure ou régulation de pression, forces, couples, puissances, études des vibrations...

Un capteur peut être étalonné directement en lui appliquant une grandeur connue. Les performances les plus élevées peuvent être envisagées sous seule condition de disposer de jauges fidèles, tant par elles-mêmes que par leurs procédés de collage. Il existe une grande variété de capteurs, Leurs principes dérivent des différents phénomènes connus de l'électricité (effets photo-électriques divers, magnéto-électricité, inductance mutuelle, etc...).

Un capteur est constitué par une pièce métallique dite "corps d'épreuve". C'est un dispositif mécanique qui, sous l'influence du phénomène à étudier, subit des déformations. Le corps d'épreuve soumis à la mesurande étudiée en assure donc une première traduction en une grandeur physique (ou mesurande secondaire); c'est celle-ci que la jauge d'extensomètrie traduit en grandeur électrique (G. ASCH, 1982).

Exemple de capteur de force

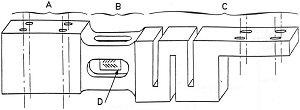
A et C : les éléments encastrés respectivement sous le plateau et sur le cadre
B : le corps d'épreuve, D : une jauge d'extensométrie

Une tendance naturelle est d'obtenir de la part du capteur, une information électrique de grande amplitude, c'est à dire un capteur dont le corps d'épreuve subit de grandes déformations. Il faut, cependant, tenir compte des performances recherchées. Des déformations trop importantes et permanentes risquent d'altérer les performances du capteur et d'engendrer des déformations plastiques (non linéaires). De plus, la linéarité du capteur dépendra de la propre linéarité de la courbe de contrainte du métal.
Le calcul d'un capteur, ou plus précisément de son corps d'épreuve, se ramène généralement à des cas simples de la résistance des matériaux (R.D.M.), traction, flexion, torsion de poutres, de membranes. (Certains métaux sont impropres à la construction de capteurs car sensibles au fluage : c'est à dire qu'ils se déforment lentement mais progressivement sous l'action de contraintes continues inférieures à leur limite élastique).

La limite élastique d'un métal est définie pour un retour au zéro donné. Généralement, le matériau choisi ne travaille qu'à un cinquième ou un dixième de sa limite élastique (ex : l'acier dont la limite élastique est de 100 daN/mm² ne sera utilisé que jusqu'à 10 daN/mm²). Un capteur peut être étalonné directement en lui appliquant une grandeur connue. Ces performances les plus élevées ne peuvent être envisagées que sous la seule condition de disposer de jauges d'extensométrie fidèles, tant par elles-mêmes que par leurs procédés de collage.

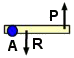
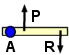
Principe de fonctionnement : Des dispositifs mécaniques particuliers peuvent provoquer la déformation du corps d'épreuve. Ainsi, par exemple, une traction F exercée sur une barre entraîne une déformation de sa longueur δL/L qui est mesurable par la variation δR/R de la résistance d'une jauge collée sur la barre.
Connaissant : d'une part l'équation du corps d'épreuve qui lie la traction, mesurande primaire, à la déformation, mesurande secondaire :

δL/L = 1/E*F/A
F/A : contrainte, A : section,  E : module d'YOUNG

et d'autre part l'équation du capteur liant sa grandeur d'entrée, ici la déformation, à sa réponse électrique δR/R soit :

δR/R = K *δL/L
K : facteur de jauge

Nous pouvons déduire la relation entre traction et variation de résistance :

δR/R = K/E*F/A

Le signal obtenu est donc lié à la grandeur physique recherchée.

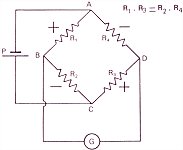En savoir plus : Le circuit de mesure électrique est généralement constitué par 4 résistances initialement égales R1, R2, R3, R4 montées en pont de Wheatstone. S'il est alimenté par une source de courant P, suivant une diagonale, nous aurons à l'équilibre une tension nulle entre B et D, par raison de symétrie. La variation de l'une quelconque des résistances fait apparaître une tension entre B et D qui peut être mesurée par un galvanomètre G. Pour de très faibles variations de résistances, ce qui est le cas des jauges, la tension de sortie (δV) est proportionnelle aux variations relatives de résistance δR/R de chacune des jauges.
Elle vaut :

δV = V/4.(δR1/R1-δR2/R2 + δR3/R3-δR4/R4)
V : tension de l'alimentation

Les signes alternés ( + ) et (-) de cette équation caractérisent la propriété fondamentale des ponts, à savoir que deux résistances opposées agissent dans le même sens, deux résistances adjacentes travaillent en opposition. D'après la règle des signes, nous voyons qu'il est possible d'ajouter ou de retrancher entre eux les effets séparés des jauges afin notamment d'éliminer les phénomènes parasites au profit d'une grandeur majorante. La tension de sortie (δV) peut être exploitée de différentes manières : Directement à l'aide d'un voltmètre ou autre système d'acquisition / Par comparaison, par méthode d'opposition, à une tension de référence / Par l'adjonction de résistances auxiliaires en parallèle sur les jauges, comme indication de déséquilibre pour rétablir la symétrie.

Calcul d'un capteur : Les règles de la résistance des matériaux (R.D.M.) servent à grouper les jauges en vue de la détection d'une composante particulière de la déformation du corps d'épreuve. Le calcul d'un capteur, ou plus précisément de son corps d'épreuve se ramène généralement à des cas simples de la R.D.M. (exemples : traction, flexion, torsion de poutres, de plaques ou de membranes).

Les formules de la R.D.M. s'appliquent à des cas idéalisés. Il ne faut pas trop s'étonner de trouver des résultats qui, bien que du même ordre de grandeur, sont parfois différents de la théorie. Par exemple, une lame fléchie travaille comme une poutre, mais près de son encastrement, elle est considérée comme une plaque. La pièce fondamentale d'un capteur est le corps d'épreuve qui subit les déformations et sur lequel sont collées les jauges. Une tendance naturelle bien justifiée est d'en obtenir une information électrique de grande amplitude donc d'avoir de grandes déformations. Il faut, cependant, tenir compte des performances recherchées.

Des déformations trop importantes et permanentes risquent d'altérer les performances du capteur et engendrer des déformations non linéaires (déformation plastique) du métal qui le compose. Nous savons par exemple que la limite élastique d'un métal ne peut être définie que pour un retour au zéro donné. Nous acceptons couramment en R.D.M., pour limite un retour à 0,2%. Suivant les caractéristiques exigées nous ne devrons "faire travailler" un matériau choisi qu'à 1/5 ou même 1/10 de sa limite élastique : ainsi, un acier dont la limite élastique est de 100 daN/mm² ne sera utilisé que jusqu'à 10 daN/mm². De plus, la linéarité du capteur dépendra de la propre linéarité de la courbe de contrainte de déformation du métal. Certains métaux sont impropres à la construction de capteur car sensibles au fluage : c'est à dire qu'ils se déforment lentement mais progressivement sous l'action de contraintes continues même inférieures à leurs limites élastiques.

Les systèmes matriciels de mesure des pressions

Les systèmes matriciels de mesure des pressions dans les contacts : dispositifs constitués d'un nombre important de capteurs de pression disposés sous forme matricielle (ils sont éventuellement être disposés à l'intérieur de la chaussure) (Cf. film)
EN CONSTRUCTION...

Accéléromètres

EN CONSTRUCTION...

Plate-Forme de Forces (ou Plate-Forme Dynamométriques)

Généralités : Les plate-formes de forces dynamométriques fournissent les 6 composantes : 3 pour les forces (F_X, F_Y, F_Z) et 3 pour les moments de forces (M_X, M_Y et F_Z) de la résultante des forces et moments appliqués sur son plateau supérieur.
Une plate-forme de forces est généralement constituée de deux structures rigides indéformables reliées par des capteurs de forces. La structure inférieure encastrée tient lieu de cadre rigide. La surface supérieure est un plateau qui sert de support aux appuis. Il restitue intégralement et sans retard les forces aux capteurs, éléments essentiels des plates-formes de forces.

Plate-forme de forces

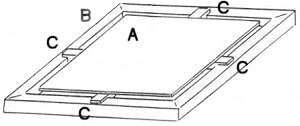
A : le plateau, B : le cadre, C : les 4 capteurs

En conclusion, connaissant :

• d'une part, la relation qui lie la contrainte sur le plateau de la plate-forme (mesurande primaire) à la déformation du corps d'épreuve (mesurande secondaire)
• et d'autre part, l'équation du capteur liant sa grandeur d'entrée, ici la déformation, à sa réponse électrique

Nous pouvons déduire la relation entre les efforts exercés sur le plateau de la plate-forme et la variation de résistance. Le signal électrique obtenu est donc proportionnel à la grandeur physique recherchée. Les capteurs peuvent détecter simultanément plusieurs paramètres.

Par une disposition judicieuse des jauges de contrainte et des capteurs de forces, les composantes d'une force exercée sur le plateau d'une plate-forme sont mesurées séparément selon les trois axes orthogonaux. Un effort F, appliqué au centre de la plaque, se répartit identiquement sur l'ensemble des capteurs. Un effort décentré provoque des moments autour des axes X, Y et Z. La valeur des forces et des moments est obtenue par des sommations ou des différences de signaux issus par les capteurs.

La Prise de Vue

La cinésiologie est l'étude du mouvement (en dehors des causes de celui-ci) par différents dispositifs comme les appareils photos à prises rapides ou stroboscopiques, les caméras cinématographiques à vitesse normale ou élevée, les caméras vidéo aujourd'hui numérique...

Le passage du film cinématographique à l'enregistrement vidéo (de env. 20 images/s à des d'obturation très faible l/4000s) permet d'obtenir des images de meilleure qualité (définition et netteté) pour des coûts bien inférieure (achat et utilisation de la vidéo) et avec une capacité de stockage accrue. Les anciens standards (VHS et Super VHS en demi pouce, UMATIC en trois quarts, et le 8mm) qui limitaient, il y a peut de temps encore, la compatibilité des images sont aujourd'hui supplanté par l'image numérique.

Aujourd'hui, l'utilisation du document enregistré est instantanée. la synchronisation est facile avec les autres sources d'informations numérique, le fonctionnement est discret (utilisation en compétition), enfin les données peuvent être utilisées directement par les systèmes automatiques de dépouillement des données.

Les Systèmes Optoélectroniques (y compris la technique vidéo), fournissent automatiquement des données spatio-temporelles en 2 ou 3 dimension à partir des données numériques issues des capteurs optiques spécifiques ou du traitement des images de caméras ou de vidéo (exemples : systèmes VICON, ELITE, ...).

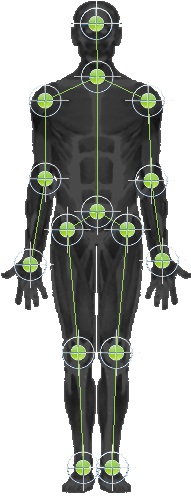
Les systèmes d'analyse de mouvements actuels sont entièrement automatiques, ils traitent en temps réel des images TV et des signaux analogiques, numérique, acquis simultanément. Le matériel est constitué par au moins 2 (en pratique 3) caméras vidéo synchronisées et travaillant généralement entre 100 et 500 images par seconde. Des marqueurs réfléchissants sont disposés au niveau des points à analyser sur un sujet d'expérience (système Elite). Le dispositif d'analyse reconnaît, pour chaque caméra, les marqueurs qu'il classe selon leur position et le modèle déterminé par l'utilisateur. Un logiciel de traitement établi une relation entre les différents marqueurs des différentes caméras, reconstruit leurs positions successives en 3 dimensions. L'exploitation des données permet d'obtenir en 3D, pour chacun des marqueurs :

• les coordonnées
• les vitesses linéaires
• les accélérations
• les déplacements dans les trois plans
• les angles, vitesses et accélérations angulaires entre deux segments préalablement définis...

Biomécanique Théorique

La modélisation est le noyau théorique de la biomécanique. C'est l'outil biomécanique le plus puissant.

Il existe différents types de modèles ; leur sélection dépend du but recherché et de l'information disponible concernant le système original (KEDZIOR et al., 1987). Dans un but de simplification, deux types de modèles seulement seront succinctement abordés ici :

• Le modèle empirico-statistique
• Le modèle théorique

Modèle empirico-statistique : Ce modèle du corps humain et de ses mouvements est utilisé pour identifier et évaluer les paramètres biomécaniques qui influencent la performance. Basé sur des données empiriques (mesures cinématiques, cinétiques, anthropométriques) et utilisant les statistiques, il cherche à déterminer d'éventuelles relations entre les paramètres choisis et la performance. Un trait caractéristique de cette approche est la suppression des relations fonctionnelles entre les variables au bénéfice de seules valeurs numériques de paramètres, qui sont dans une certaine mesure, sélectionnées arbitrairement. Ce modèle n'est justifiable que par des applications pratiques réussies.
Précédemment menée comme une approche "canon", la procédure a été complètement redéfinie (HAY et REID, 1982) de la manière suivante. Le modèle est composé de "quantités" mécaniques à différents niveaux, et arrangé de telle manière que les facteurs d'un niveau déterminent totalement les facteurs du niveau directement supérieur. Les relations entre les différents niveaux ou les "quantités" mécaniques ne sont cependant pas décrites sous forme d'équations algébriques ou différentielles, mais en bloc-diagramme. Cette caractéristique exprime le manque de relations quantitatives entre les variables. Ainsi, le modèle ne peut donner l'assurance que les variables d'entrée sont indépendantes les unes des autres. On peut donc se poser la question de savoir si le modèle est déterminant. Gardant ceci à l'esprit, on peut l'utiliser comme approche pragmatique pour sélectionner des facteurs importants au moyen de relations statistiques.

Modèle théorique : Ce type de modèle se base sur les connaissances théoriques des structures et fonctions mécaniques du corps humain. On peut établir une hiérarchie de modèles suivant leur niveau de complexité (KEDZIOR et al., 1987) :

• modèle mécanique
• modèle musculo-mécanique
• modèle neuro-musculo-squelettique

Ils peuvent servir de modèle original pour le corps complet ou tout sous système, prenant en compte les conditions environnementales. Un modèle très simple est généralement utilisé pour déterminer les moments articulaires et les forces internes globales au niveau d'une articulation.
Il est évident que le modèle utilisé en raison de l'activité musculaire incontrôlée des antagonistes et de la non-connaissance de la distribution des forces entre les muscles bi-articulaires ou les muscles mono-articulaires peuvent fournir des résultats plus ou moins erronés, et sans intérêt pour des buts pratiques. Pour surmonter cette faiblesse, des procédures d'optimisation mathématiques ont été scientifiques ont été utilisées.
Ces méthodes sont des outils utiles pour l'analyse de systèmes complexes qui fonctionnent suivant certains principes.
La question fondamentale est : "Quels principes peuvent être choisis comme fonctions objectives, comme d'optimisation ayant une signification biologique ?"
EN CONSTRUCTION...

Eléments de Mécanique Humaine

Particularités de la Machine Humaine

On ne dispose pas des plans précis du corps humain, alors même qu'il existe une grande variabilité interindividuelle : Forme Dimensions Résistance mécanique, fonctionnelle, physiologique Capacités fonctionnelles, cognitives, motrices Evolution / vieillissement des caractéristiques en fonction du temps Réactivité et adaptation face aux stimulus / aux agressions extérieures Optimisation liée à l'évolution Réponse à l'entraînement...

Homme de Vitruve De vinci

Du point de vue du biomécanicien, le corps pourrait se décomposer de la façon suivante :

Structures humaines	Fonctions	Equivalent mécanique
Os, squelette	Porter, supporter, donner une forme	Structure, carrosserie
Articulations	Déformation de la structure	Axes
Tendons	Maintient de la cohésion de la structure	Liaisons mécaniques
Muscles	Création du mouvement, stabilisation du corps	Moteurs

Centre de gravité humain

	Structure	%  du poids total	Localisation de Centre de Gravité
	Tête	6,9 %	Selle Turcique ou fosse sphénoïdale
	Cou	1,9 %	Extrémité inférieure de l'os occipital
	Tronc	51,1 %	Face antérieure de L1
	Tête + Cou + Tronc	59,9 %	Face antérieure de T11
	Bras	2,7 %	Partie moyenne de l'humérus
	Avant-bras	1,6 %	Au-dessus de la partie moyenne de l'avant-bras
	Main	0,6 %	Partie moyenne du 3ième métacarpien
	Membre sup.	4,9%
	Cuisse	9,7 %	A la base du 1/3 sup du fémur (bord médial)
	Jambe	4,5 %	A la base du 1/3 sup du tibia (face postérieure)
	Pied	1,4 %	Au niveau post-inf de l'interligne C2 -C3
	Membre inf.	15,6%
	Corps humain	100 %	env. = Corps de S2 en position de référence anatomique

 

Les os

EN CONSTRUCTION
206 os en remaniement permanent (Ostéoblaste : fabriquent l’os (Ca+) Ostéoclaste : détruisent l’os)

Fonction de soutien / protection / support leviers (Mvt) / forme

Reliés entre eux (X°), tissu vivant : vascularisés et innervés
Os : Caractéristiques mécaniques
Elastique : soumis à une F, il se déforme, puis retrouve sa forme initiale. ≠ selon facteurs (âge, sexe, mobilisation prolongée)
Hystérésis parfait = Pas de déformation résiduelle, mais il peut y avoir fatigue du tissu osseux (si sollicitation répétée)  retour plus long dans le temps
Sec : + cassant, rupture après ph. élastique
Module d’élasticité (de Young, en N/m² ou kg/mm²) rapport contrainte-déformation = L/L.F/S  env. 2000 kg/mm² (acier 20 000, bois 1 000)
Os : Caractéristiques mécaniques
+ module de young grand, + corps "raide" (peu élastique)
L’os compact à un module d’élasticité > à l’os spongieux
Le module de l’os est moyen (faible), os = tissu relativement souple

Les contraintes de flexion ou de rotation s'exercent surtout à la périph (os creux)

Os+ muscle = poutre composite
Os
Propriétés mécaniques ≠ selon directions (Anisotropie)
os long : élasticité dans le sens longitudinal = 2 fois > élasticité sens transversal. Os plus résistant en compression car prédisposé

La direction des travées osseuses 
semble augmenter  les qualités
mécaniques dans le sens longitudinal

Résistance à la rupture dépend de 5 facteurs :
Section / épaisseur / architecture / configuration ext / qtté sels minér
ex : rotule : 198 kg, tibia : 450 kg, fémur : 756 kg

Résistance à la fatigue (application =  ½ charge de rupture)
nombre de cycles = 1 à 2.8 milliards (ex. : acier = 107 cycles)
Os
Légèreté
Os non plein, Teneur en eau augmente poids (squel sec = env. 6/7kg)

Variations
Age dés 25 ans résistance  (traction, compres, flexion)  composition histologique évolue
Sexe  femme : risque  résistance os : ostéoporose post ménopause (processus hormonal)
Immobilisation :  caractéristiques mécaniques (os non soumis à G est + élastique - Cf. astronautes)

Malnutrition
Vascularisation osseuse
Facteurs héréditaires

Cartilage
Tissu ferme, légèrement dépressible, élastique, surface excessivement lisse
75% d'eau : fibres collagène, gel de protéoglycanes hydrophiles (protéine), de chondrocytes (responsables synthèse de la matrice)
2 rôles
fonction dynamique (+ liq synovial) =  F de friction
fonction statique = transmission, répartition pressions & amortissement contraintes
Cartilage
Coef de frottement = F/N
Glisse 10 à 100 fois + que le nylon sur l'acier


Cartilage
Contraintes écrasantes  NRJ de rotation
Elasticité (amortissement), solidité et auto nutrition dues à la structure moléculaire du tissu
Cartilage poli  autonomie motrice de l'être vivant (au même titre que l'autonomie métabolique et mentale - P. Vendryes)

Défaut : Faible capacité de régénération en cas de lésions

Les muscles

EN CONSTRUCTION
Propriétés
Contractilité / Elasticité / tonicité
non également réparties

Formes
Fusiforme / penné / segmenté / large
Section physiologique  Fmax
W dans 3 types de leviers (Cf leviers)

Muscles
(5) Composante élastique passive
Tissu conjonctif du corps musculaire
(4) Composante contractile
Fibres musculaires contractiles génératrice de F
(6) Composante visqueuse
Transfert liquidien du muscle = amortisseur visqueu
Muscles
Muscles
Muscles du déplacement
Forme : Longs, fins, fusiformes : fibres = direction muscle  déplacement
Où : Extrémités, squel distal = mbres
Typologie : Fibres blanches (FT) rapides  dans des leviers IP privilégient vitesse & déplacement à force. F élastiques, peu toniques, fortement et rapidement contractile, mais fatigable
S'entraînement : Contractions dynamiques : efforts max. à vit ++
Muscles du maintien
Forme : Courts plats compacts svt penné : fibres ≠ direction muscle  puissance
Où : Squ proximal, tronc, gouttière vertébrale (fessiers, abdo). Posture
Typologie : Fibres rouges (ST) fibres lentes  dans des leviers IR privilégient force à vitesse & déplacement. F peu élastiques, très toniques. Gde résistance à la fatigue
S'entraînement: Efforts sous max. de longues durées, nbreuses répétitions

C4/ Tendons
Tendons
Tendons
Données évolutives
la surface de section du tendon n’augmente plus à l’âge adulte
la résistance à la traction est modifiée par l’exercice ou l’immobilisation

le tendon se modifie avec l’âge :
taille cellules, teneur en eau diminuent
élasticité et résistance diminuent


Role stabilistaur ou moteur d'un muscle en fonction du point fixe

Les articulations

EN CONSTRUCTION

C5/ Articulations
Epaule
S'oppose à la hanche
Evolution par libération de l'appui
Appui…suspension…libre
Mobilité + stabilité - : luxation plus fréquente
Peu d'arthrose car peu d'usure
Préhension : Biceps = muscle nourricier (Flexion totale mbre > = prise + amener à la bouche)
Epaule
Action deltoïde   humérus
Sus-épineux = fixe tête hum. +  limite ascension
Abduction = mise en jeu muscles abaisseurs (sous-scapulaire, sous-épineux, grd pectoral, grd dorsal)
Ensemble = couple de rotation  abduction
Epaule
Paradoxe de Codman
Bras le long du corps (pouce en DH)
Abduction
Flexion horizontale
Déflexion ou Extension vers position 
de référence anatomique
 Cf. main (pouce en …)
Coude
Articulation intermédiaire du membre thoracique
Porter la main à la bouche (valgus)

Complexe du coude = 3 X°
Déport en AV de la palette hum 30°
Axe trochlée vers le HT et le DH de 10° cubitus valgus
LLI : fais.ant tendu en ext., fais post tendu en flexion
LLE : tjrs tendu sur lig annulaire
Coude : solutions biologiques
Coude
Stabilité max à 90° de flex.
Secteur utile en av : amplitude 80 à 100°
Courbure pronatrice Radiale en manivelle
Biceps brachial est supinateur (enroulé sur la tubérosité bicipital du radius en pronation)  traction
Hyper extension laxité de 5 à 10°

3 repères osseux :
olécrane / épitrochlée / épicondyle
Poignet
Rappel anat : Canal carpien avec fléchisseurs + nerf médian

Prise  :
Nerf radial : ouverture
Nerf médian : prise fine
Nerf ulnaire : tenue solide
Poignet
2 rangées d'os liés par lig. intra-capsulaire, pas les rangées (la 1ere rangée ne reçoit presque pas muscle = "ménisque" de la 2°)

2 articulations radio-carpienne (flexion surtout) et médio-carpienne (extension surtout)
Médio-carpienne limitée en rotation par lig et tendon flechisseur  verrouillage mais prono-supination = bon compromis entre stabilité et mobilité, stable dés que muscles de l'av-bras contractés c à d main utilisée

Flexion + adduction / extension  + abd
Main
Axe abd/add = 3ième doigt
Arches digitales = main creuse
Opposition du pouce à tous les doigts (uniq.)
En flexion : axe fermeture doigts vers trapèze = pronation automatique
Muscles extrinsèques moteurs dans l'av-bras
Pouce : 2 phalanges + liberté commence à M1 (X° en selle entre trapèze et M1)

Tabatière anatomique. Scaphoïde (fracture immobil. = 2 mois car partie médiale mal irriguée, plâtre = main + coude)
Evolution métacarpe chez mammifères
Préhension
Main = outil multiprise adaptatif

Pince digital / interdigt.
Adhérence
Empaumement
Avec ou sans opposition I
Serrage latéral

Hanche
Dédiée Marche : stabilité (+) / mobilité (-)
Utilité 20 à 30° dans la marche
Le membre inf se verticalise
Hanche
Usure avec le temps
importance du sourcil 
(ou toit)
Angle  diminue avec âge
Fémur regarde vers l'AV et 
Cotyle vers l'av !
Hanche
Mouvement
Dépend de la position du genou (si fléchi + d'amplitude), 90° à 120° voir 140° en passif (160° "prière mahométane")
Position instable

"Grand écart ant." possible car bascule ant bassin + hyperlordose
Abduction des mbres inf max 60° : "grand écart facial" possible car fexion hanche bascule ant bassin + hyperlordose

Biom accouchement
Contre nutation
passage du détroit sup.
Nutation
 passage du détroit inf.


Le coccyx aussi
Genou
Le poids exerce une contrainte
proportionnelle a la charge
et inversement proportionnelle
à la section de la surface
portante

Dans le genou la charge
est déportée en DD
Genou
Des contraintes de flexion (2) s'ajoutent aux contraintes de compression (1) pour 
donner le diagramme (3)

Dble condylienne  contraintes
en flexion s'annulent
Genou
Modèle : Colone articulaire de genou
P axe poids du corps
(A) = hauban
(B) = augment°
de la surface
portante

Genou
Besoin de stabilité

Hyper recurvatum (ext 5 à 10 °) / genu valgum (en "X") / genu varum (axe tibia vers DH)
Arthrose (usure) du genou dés 75 ans frq
X° sous cutané peu/pas protégée
Rotule = os sésamoïde
Asymétrie plateau T. (convexe ext; concave int) rotation axe condyle creux
Asymétrie condyle lat + long  rotation externe en ext & rotation int en flexion
Genou
Genou tendu  came de grd diametre  lig lat. tendus  stabilité +

Ménisques pour améliorer congruence
ménisques attachés à rotule : l'extension les ramène vers AV
LLI (lame vers BAS) et LLE (corde vers ARR) se croise dejà
LCAE (+vert) & LCPI (+horiz) toujours tendus sinon "tiroir". Ils s'enroulent en rot int
LC et LL se croisent en X  stabilité
Principes biom du genou
MOUVEMENT
Extension  n'existe pas (position anat de ref)
Flexion dépend de position hanche : si hanche ext 120°, hanche en ext 140°, passive 160°
Extension forcée subluxation rotule (vers ext) (vaste int trop faible : frq aux Antilles)
En flex  ménisque recule (maladie des carreleur : à la levée le ménisque pas le temps d'avancer)
Pas besoin de rotation en ext car rot. hanche
Genou
Genou
Genou
Surfaces portantes du genou
Cheville
Pied = voûte plantaire

 3 points d'appuis (tête MI (33.3%) et MV (16.6%) et calcanéum (50%))
3 voûtes (ant. / médiale + HT / latérale + BAS = 1er amortisseur (pas d'amortis. chez paraplégique)

Cheville
Péronier ant (3° fibulaire)
Ext com orteils
Ext propre gros orteil
Jambier ant (tibial ant)
Jambier post (tibial post)
Flé comm orteils
Flé propre gros orteil
Triceps sural
Lg péronier lat (lg fibulaire)
Court Péronier lat. (court fibulaire)
Cheville
Flexion dorsale stable / flexion plantaire instable (poulie de astragale (talus) plus large en av)
Axe talus 15° vers DD par rapport
au pied car car jambe en DH

Lig en Y de chopart sur l'interligne de
 chopart (amputation)

Cheville
Empreintes:
Normal
Creux
Pied bot varus équin
Pied plat
Pied bot talus valgus
Cf. usure chaussure

Pied grec (II plus grand) + fréquent
Pied égyptien (I plus grand)
Pied carré
Cheville
Cheville

L'avant du pied en vrille :  articulation de Chopart (2)

Articulation de Lisfranc (1)

Cinématique

définition

La Cinématique est l'étude du mouvement dans le temps sans se soucier des causes de ce mouvement. C'est une analyse descriptive et temporelle du mouvement. Cette description s'énonce en terme de déplacement, de vitesse, d'accélération, de trajectoire et dépend donc du référentiel choisi. En STAPS, l'analyse cinématique d'un geste, d'une action motrice, d'un mouvement, s'effectue le plus souvent, en fonction du référentiel terrestre (ou Galiléen).

Equations du mouvement dans un espace a une Dimension

Vitesse (m/s)

On dit d'un objet qui change de position en fonction du temps qu'il a une vitesse.
Vitesse moyenne :

V_moy = (x_f-x_i) / (t_f-t_i) = δ(x) / δ(t)
x_f : position finale ; x_i : position initiale ; t_f : temps final, t_i : temps initial

Vitesse instantannée : limite de la vitesse moyenne lorsque δt tend vers 0 (en m/s)

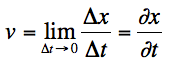
Accélération (m/s²)

On dit qu'un objet dont la vitesse varie avec le temps qu'il possède une accélération. s'il elle est positive, l'objet accélère, si elle est négative l'objet freine.
Accélération moyenne :

a_moy = (v_f-v_i) / (t_f-t_i) = δ(v) / δ(t)
v_f : vitesse finale ; v_i : vitesse initiale ; t_f : temps final, t_i : temps initial

accélération instantanée : limite de l'accélération moyenne lorsque δt tend vers 0 (en m/s²)

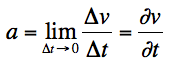
Dans le cas d'un mouvement uniformément accéléré, le mouvement est dit uniformément varié : MUV
Dans le cas d'un mouvement à vitesse constante, le mouvement est dit rectiligne uniforme : MRU
Pour simplifier la notation, on peut supposer que le temps de départ est nul (temps à l'origine) : t_i = 0 et on note t le temps écoulé (à la place de t_f)
La position initiale (x_i) et la vitesse initiale (v_i) seront notés x₀ et v₀. Au moment t, elles sont noté x et v (à la place de x_f et v_f)

1. v_moy=(x-x₀)/t => x=x₀+vt
2. v_moy=(v+v₀) =>
3. a_moy = (v-v₀)/t => v=v₀+at

Cas de la chute libre
v₀=0, x₀=0 et l'accélération est égale à l'accélération gravitationnelle, g soit (9,81 m/s²). Les 3 précédentes équations deviennent :

1. x=vt
2. v=at
3. x=1/2gt²

Equations du mouvement dans un espace a 2 ou plusieurs Dimensions - Vecteurs

En physique, il existe 2 types de grandeurs :

• Les grandeurs scalaires ou valeurs numériques suivi de leur unité : ex. temps (s), distance (m)...
• Les grandeurs vectorielles qui sont définies par :
• une intensité
• une direction
• un sens

Comment représenter un vecteur ?
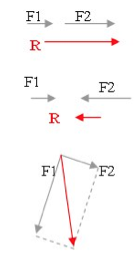
Les vecteurs sont représenté par une flèche, avec un point d'application, une droite d'action ou de support, une direction (celle de la droite de support), un sens (celui de la flèche) et une intensité (longueur de la flèche ou plus précisément "grandeur de son module")

Dans un système cartésien, un vecteur V peut être représenté par sa grandeur (intensité) et l'angle formé avec l'axe des X, ou par ses composantes V_X et V_Y.

EN CONSTRUCTION
Opération graphique avec des vecteurs
On dit d'un objet qui se déplace en décrivant un cercle à une vitesse constante v qu'il exécute un mouvement circulaire uniforme
Même si la grandeur de la vitesse demeure constante, sa direction varie continuellement.

 L'accélération étant définie comme le rythme de variation de la vitesse, une variation de la direction de la vitesse correspond à une accélération au même titre qu'une variation de sa grandeur.
 
 Ainsi, un objet qui effectue un mouvement circulaire uniforme accélère. Cette accélération est dirigée vers le centre du cercle On parle d'accélération radiale ou centripète.
ar = v² /r

Dynamique

Lois de Newton

1ière loi de Newton	2ième loi de Newton	3ième loi de Newton
Un corps reste immobile ou conserve un mouvement rectiligne uniforme aussi longtemps qu'aucune force extérieure ne vient modifier son état (loi d'inertie). Inertie : Propriété d'une masse qui présente une résistance, à l'accélération ou à la décélération, appliqué par des forces externes - Un solide ne se met pas spontanément en mouvement - Un solide en mouvement ne s'arrête pas de lui-même, il tend à conserver indéfiniment la direction et la vitesse de son mouvement rectiligne et uniforme (sur terre, des forces de frottements ralentissent puis arrêtent les mouvements)	L'accélération (a) d'un objet est directement proportionnelle à la force exercée sur lui (F) et inversement proportionnelle à la masse de celui-ci (m) La direction de l'accélération correspond au sens dans lequel la force s'exerce. a=F/m => F=m.a	Chaque fois qu'un objet exerce une force sur un second objet, celui-ci exerce en retour une force égale mais opposée. A chaque action correspond une réaction égale intensité, mais de sens opposé.

Forces

On appelle force toute cause ou action susceptible de modifier le mouvement d'un corps, de le déformer. Il s'agit donc d'un facteur qui tend à modifier l'état d'inertie de celui-ci. Une force communique une donc accélération (positive ou négative) à une masse ou à un point matériel. Il peut donc s'agir soit :

• De la mise en mouvement d'un corps initialement au repos,
• De changer la trajectoire et/ou la vitesse d'un corps en mouvement
• De modifier l'état d'un corps sans qu'il y ait mouvement (déformation)

Caractéristiques
Une Force F est représentée par un vecteur avec :

• Une flèche
• Un point d'application (par ex. l'insertion d'un muscle sur le segment mobile)
• Une direction : varie selon le type de muscle, sa (ses) terminaison(s)
• Un sens : celui de la traction du muscle (que représente la flèche)
• Une intensité exprimée en Newton (N), qui dépend du W du muscle (que représente la longueur de la flèche)

En Mécanique humaine, les forces internes sont les contractions musculaires exercées sur les segments osseux pour les mobiliser ou les stabiliser. Des forces externes peuvent s'ajouter ou s'opposer aux forces internes. Force musculaire résulte de la contraction musculaire qui peut être :

• Isométrique : il n'y a pas de mouvement perçu. Travail musculaire de maintien. Les insertions musculaires ne se déplacent pas
• Concentrique  : il y a un mouvement (travail musculaire moteur). Les insertions du muscle se rapprochent.         
• Excentrique  : il y a un mouvement mais dans le sens opposé au raccourcissement du muscle. C'est une contraction frénatrice, un travail freinateur. Les insertions musculaires s'éloignent.

Inertie
Propriété d'une masse qui présente une résistance, à l'accélération ou à la décélération, appliqué par des forces externes. Un solide ne se met pas spontanément en mouvement, un solide ne s'arrête pas de lui-même mais tend à conserver indéfiniment la direction et la vitesse de son mvt rectiligne et uniforme


Addition vectorielle
F = vecteur caractérisé par
point d'application : l'insertion sur le segment mobile
direction : varie selon le type de muscle
sens : celui de la traction du muscle
intensité : dépend du W du muscle


Décomposition d'une force : Cf trigo

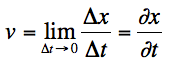
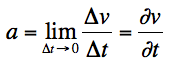
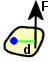
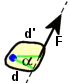
Sinα = côté opp / hypo
Cosα = côté adj / hypo
tanα = sinα /cosα = côté opp / côté adj

 EN CONSTRUCTION
Addition Vectorielle
Décomposition d'une force

Pesanteur

La Pesanteur est l'action de l'attraction terrestre (g) : c'est une force verticale dirigée vers le bas qui s'exerce sur tout corps de masse m. En absence de mouvement, cette action correspond au poids et elle est proportionnelle à la masse :

P=m.g
P : poids (N), m: masse (kg), g: gravité (9,81 N/kg ou m.s^-2)
(Cf. 2° loi de Newton, F=ma)

La pesanteur peut-être représenté par un vecteur qui aura pour caractéristiques :

• Lieu d'application : le centre de gravité
• Direction : verticale
• Sens : vers le BAS
• Intensité proportionnelle à la masse : m.g

.

Leviers

Définitions

Un levier est une barre rigide, mobile autour d'un point fixe (point d'appui, axe de rotation) et soumis à 2 forces qui tendent à le faire tourner en sens opposé.

On peut choisir arbitrairement un sens de rotation positif : une force aura une action positive, l'autre aura une action négative, ces 2 actions peuvent s'annuler créant ainsi un équilibre.

On note généralement :

• P (puissance) la force active du sujet, c'est la force musculaire (la pesanteur peut s'y ajouter si elle agit dans le sens du mouvement),
• R la résistance (résistance) la force qui résiste au mouvement, C'est généralement un force externe au corps (pesanteur, force extérieure, résistance de muscles antagonistes, tensions ligamentaires...),
• A le point d'appui c'est à dire l'axe de rotation, le sens de rotation positif est traditionnellement le sens horaire.

Force : La force appliquée à un corps est ce qui modifie ou tend à modifier l'état de ce corps. Une force peut tendre à accélérer, freiner la vitesse d'un corps, changer sa direction ou le déformer. Un force est caractérisée par un vecteur lui même caractérisé par son intensité, sa direction et son sens. Unité : N (le Newton), 1N permet de déplacer une masse de 1kg par m/s²

Intensité d'une force : c'est l'action plus ou moins grande avec laquelle elle agit (la force musculaire humaine est en rapport avec le nombre et l'épaisseur des faisceaux qui se contractent - Cf. Section physiologique).

Bras de levier : c'est la distance (d) qui correspond à la perpendiculaire abaissée de l'axe de rotation sur la droite de direction de F (soit, la  distance entre axe de rotation et droite support du vecteur force, comptée perpendiculairement à la direction de cette force).
Unité : le m (mètre)

bras de levier = d

bras de levier = d=d'.sinα

  Rappel trigonométrie :

sinα  = côté opposé/hypoténuse
cosα  = côté adjacent/hypoténuse
tanα  = sinα/cosα = côté opp/côté adj

α	0°	30°	45°	60°	90°
cosα	√4/2 =1	√3/2	√2/2	√1/2 =1/2	√0/2 =0
sinα	√0/2 =0	√1/2 =1/2	√2/2	√3/2	√4/2 =1

avec √2=1.414 et √3=1.732

Moment de force (M_F) : C'est le produit de l'intensité de la force par son bras de levier. Il rend compte de "l'efficacité" de la force en rotation. Plus le bras de levier est long, plus la force nécessaire pour permettre une rotation sera faible.
Le moment d'une force représente donc son aptitude à faire tourner un système mécanique autour d'un point donné (le signe dépend du sens de rotation positif initialement choisi).
Une force dont la direction passe par l'axe de rotation n'engendre pas de rotation : son bras de leviers est nul donc son moment est nul.
Unité : le Nm (Newton.mètre)

MF=F.d car sin90°=1	MF=F.d ou MF=F.d'.sinα

Types de leviers : Il existe 3 différents types

Description	Levier Inter-appuis (ou levier du 1° genre) L'axe ou le point d'appui (A) se situe entre les points d'application des forces P et R	Levier Inter-résistant (ou levier du 2° genre) R se situe entre P et A Leviers rares dans le corps humain bien qu'ils favorisent la puissance musculaire	Levier Inter-puissant (ou levier du 3° genre) P se situe entre  R et A Leviers les plus nombreux dans l'appareil locomoteur.
Exemples physiques
Exemples anatomiques
Exemples mécaniques
Avantages/ inconvénients	pour atteindre l'équilibre : l'intensité de P peut être égale à celle de R, si leurs bras de levier sont de mêmes longueurs	Efficacité de P (++) en effet, P peut équilibrer R malgré une intensité moindre car son bras de levier est plus grand Amplitude du mouvement provoqué par P (--) car loin de l'axe, P n'engendre que peu de déplacement	Efficacité de P (--) pour équilibrer R, P doit avoir une intensité supérieure à R car son bras de levier est plus petit Amplitude du mouvement provoqué par  P (++) car près de l'axe, P engendre un plus grand déplacement de l'extrémité du segment

Effet des muscles sur les leviers

Démonstration : à l'équilibre

∑M=0
donc M_P+M_R=0
soit (p.P)+(r.-R)=0
(ici le moment de R est négatif, sens antihoraire)
p.P=r.R
P=(r/p).R

- A l'équilibre : il n'y a pas de déplacement, la somme des Moments (M) de forces est nulle : M_P+M_R=0 d'où P doit être égale à (r/p).R

• Dans le cas d'un levier de type inter-appui r/p peut être égal à 1, dans ce cas pour l'équilibre, il suffit que P soit égal à R
• Dans le cas d'un levier de type inter-puissant : r/p est supérieur à 1 (donc défavorable), donc pour obtenir l'équilibre, il faut que l'intensité de P doit être plus grande que celle de R

- Déséquilibre :

• Le muscle exerce un travail concentrique (ou contraction concentrique) si, en se contractant, il se raccourcit (c'est à dire rapproche ses insertions), dans ce cas : P > (r/p).R
• Le muscle exerce un travail excentrique (ou contraction excentrique) si il s'allonge malgré une contraction (ses insertions s'éloignent, il joue le rôle d'un frein au mouvement, à la rotation, qui dans ce cas est créé par la résistance), dans ce cas : P <(r/p).R
• Dans le cas d'un équilibre (travail statique) le muscle exerce un travail isométrique (ou contraction isométrique) : P=(r/p).R

Leviers et application

exemple du deltoïde