Fig 1 Two layer perceptron
1. Introduction As Stork & Allen [2] noticed, there are no fast and hard rule as to the number of hidden units required in a three layer perceptron. But, in a two layer perceptron, the layers are directly specified by the problem. It is then interesting to use a two layer perceptron if it is able to separate non linearly separated sets of data. This will be possible if the activation function is non monotonic. Periodic activation function have already been used, by Brady [3] or Gioello & Sorbello [4] for instance, but always in a 3 layer perceptron. Consider a 2 layer perceptron, the input layer containing 2 cells, the output layer one cell , which tries to recognise the Xor boolean function..

Fig 1 Two layer perceptron
Let us assume that the activation threshold is S for each cell. If C1 and C2 are the synaptic weights between input cells and the output cell, the entry array (0,0) gives the result 0. If the two arrays (0,1) and (1,0) must give the response 1 then C1>S and C2>S. But then the activity of the output cell is C1+C2>2*S>S when the input is (1,1) and the result is false. If we assume that the cells have two thresholds, S1 and S2, with the response 0 if activity is less than S1, 1 between S1 and S2 and 0 after S2, the XOR problem can be solved if S1<C1<S2, S1<C2<S2, and (C1+C2)> S2 .

Fig 2 Two-thresholds activation function
It is easy to see that one can choose C1 and C2 to solve OR and AND problem : For the AND problem, C1<=S1, C2<=S1 and S1<C1+C2<S2 gives a correct answer. One can chose C1=C2=S1/2+ , S2>S1+2*, S1>0 to have the good values. For the OR problem, S1<C1<S2, s1<C2<S2, and S1<(C1+C2)<S2 are necessary, so one can choose C1=C2=S1+, and S2>2*(S1+). When you chose good values for S1 and S2, this perceptron can solve the three Boolean operations.
2. From two thresholds neurones to multi thresholds neurones. It may be difficult to choose the good values for the threshold, for a given problem. Perhaps is it possible to change the threshold values during learning, but it seems simpler to have an infinity of thresholds, with alternatively 0 and 1 responses. Such a neurone could be compared to a fork with an infinity of slots which give the response 1. A new problem raises: what is the optimal with of the slots and what about the learning strategy? We will study this points with periodic neurones: The activation function is defined by:
O= odd(truncate (A)) where A= (Ci x Ei) , Ci is the weight on synapse from the cell i in the input layer, Ei the value (0 or 1) of this cell . Where odd gives 1 for odd values else 0. This gives an infinity of slots with width=1, and a slot of with 1 each side of zero.

Fig 3: multi threshold activation function
The next problem is the training of a two layer perceptron which each cell of the output layer is a periodic neurone. For each cell in the output layer, if the activity is not correct, we have to modify the synaptic weights of the links leading to this cell from actives cells of the first layer. We modify the weights in order to increase or decrease A to reach the nearest good slot: for example, if we find that A=1.7 (O=1) and want to have O=0 then we have to increase A up to 2+ . We dispatch the correction regularly over all weights leading to this cell: if there are 3 weights to correct, each will be increased of (2+ -1.7)/3 . To avoid oscillations we introduce a random factor in the correction . In our example each weight will be increased of (2+ - 1.7 +r)/3 where r is a random value in [ 0..1 [ .
3. Some experiments with a periodic perceptron. We have tested this model with several problems.
· The first one is the XOR problem: The Neural Network is very simple: two input cells and one output cell:
Fig 4 Xor periodic perceptron
Test Ndeg. 1
Epoch 1 3 errors C1= 0.558643 C2= 0.181427
Epoch 2 2 errors C1= 0.654978 C2= 0.339543
Epoch 3 2 errors C1= 1.405688 C2= 1.277607
Epoch 4 0 errors C1= 1.405688 C2= 1.277607
Test Ndeg. 2
Epoch 1 2 errors C1= 0.351805 C2= 0.110382
Epoch 2 3 errors C1= 0.508447 C2= 0.431842
Epoch 3 3 errors C1= 0.645629 C2= 1.066659
Epoch 4 1 errors C1= 1.198431 C2= 1.066659
Epoch 5 0 errors C1= 1.198431 C2= 1.066659
· The second is the parity problem. The input layer has 16 binary cells, the output layer only one which value is 1 if and only if the number of input cells with value 1 is even, else 0. The training stage is much faster than with a 3 layer perceptron and backpropagation learning. Here are the results of a test sequence with the number of errors in each epoch and the synaptic values after training :
Test Ndeg.1
Epoch 1 Errors =42314 Epoch 6 Errors =8 Epoch 10 Errors =2 Epoch 2 Errors =42266 Epoch 7 Errors =6 Epoch 11 Errors =4 Epoch 3 Errors =18348 Epoch 8 Errors =6 Epoch 12 Errors =1 Epoch 4 Errors =47 Epoch 9 Errors =4 Epoch 13 Errors =0 Epoch 5 Errors =17final values of synaptic weights
-1.002 -1.170 -1.052 -1.026 -1.110 -1.066 0.842 0.998
-1.031 0.973 0.938 -1.031 0.964 -1.007 -1.032 0.838
---------------------------------------------------------------------------
Test Ndeg.2
Epoch 1 Errors Epoch 5 Errors Epoch 9 Errors Epoch 13 =42236 =42406 =15 Errors =8 Epoch 2 Errors Epoch 6 Errors Epoch 10 Epoch 14 =42452 =42159 Errors =9 Errors =6 Epoch 3 Errors Epoch 7 Errors Epoch 11 Epoch 15 =42179 =183 Errors =3 Errors =2 Epoch 4 Errors Epoch 8 Errors Epoch 12 Epoch 16 =42166 =24 Errors =7 Errors =0
final values of synaptic weights
-1.179 -1.035 -1.045 -1.153 -1.001 -1.053 -3.021 -1.002
-1.023 -1.005 -3.045 -1.074 0.998 2.962 -1.057 2.770
---------------------------------------------------------------------------
Test Ndeg.3
Epoch 1 Errors =42283 Epoch 4 Errors =19 Epoch 7 Errors =1 Epoch 2 Errors =42328 Epoch 5 Errors =22 Epoch 8 Errors =0 Epoch 3 Errors =5529 Epoch 6 Errors =8final values of synaptic weights
-1.025 -1.022 -1.099 -1.046 -1.005 -1.038 -1.037 -1.015
0.926 -1.006 0.996 0.979 0.995 -3.001 2.786 0.628
· The third problem is a pattern recognition problem: We want to recognise the ten digits, each of them is represented in a 12x12 matrix of dots and looks like a digital calculator display :

Fig 5 models of digits

Fig 6 disturbed inputs, N=22
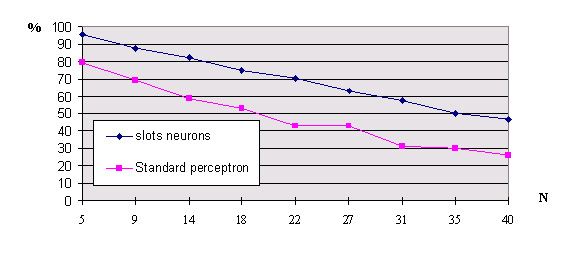
Fig 7 percent of good answers with noisy inputs
4. Conclusions. The two layer perceptron with periodic neurones which can solve Xor type problems can replace MLP in many situations. The learning time is short, the generalisation abilities are good and the structure of the network is completely determined by the problem: there is no more hidden layer witch size is always empirically chosen. The size of the input layer is determined by the input data and the output layer by the results. The only parameter to tune is the random factor of the learning algorithm which can be do easily by a few attempts. As an example, we use a two layer periodic perceptron to do speech synthesis in guadeloupean creol from texts [5]: with a classical three layer neural network the training stage with 52 sentences was wery long. more than 12 hours were necessary to learn (with a 486 PC). The periodic perceptron performs the learning in only 6 minutes. Moreover, the generalisation ability of the periodic perceptron is better (95%) than the classical MLP (90%).
Refernces:
[1] M. Minsky, S. Papert Perceptrons: An introduction to computational geometry. Cambridge, MA:MIT Press 1969
[2] D.G. Stork, J.D. Allen How to Solve the N-Bit Parity Problem With Two Hidden Units Neural Networks vol 5 Ndeg. 6 nov-dec 1992
[3] M.J. Brady Guaranteed learning algorithm for networks with units having periodic threshold output functions. Neural Computation vol 2 p 405-408 1990
[4]M. Gioello, F. Sorbello A new VLSI neutal device with sinusoidal activation function for handwritten classification Neural Networks & Their Applications Marseille 20-22 mars 1996
[5] B. Filliatre, R. Racca Synthèse vocale du creole par un réseau de neurones 8deg. colloque international des études créoles Pointe à Pitre 6-10 mai 1996